缓和曲线是用于连接直线和圆曲线、圆曲线和圆曲线间的过渡曲线。它的曲率半径是沿曲线按一定的规律而变化的。设置缓和曲线使直线和圆曲线之间、圆曲线和圆曲线之间的连接更为合理，使车辆行驶平顺而安全。

1）缓和曲线的性质

车辆在曲线上行驶会产生离心力，所以在曲线上要用外侧高、内侧低呈现单向横坡形式来克服离心力，称弯道超高。离心力的大小与曲线半径有关，半径愈小，离心力愈大，超高也就愈大，故一定半径的曲线上应有一定量的超高。此外，在曲线的内侧要有一定量的加宽。因此，在直线与圆曲线和两个半径相差较大的圆曲线中间，就要考虑如何设置超高和加宽的过渡问题。为了解决这一问题，在它们之间采用一段过渡的曲线。如在与直线连接处，它的半径等于∞，随着距离的增加，半径逐渐减小，到与圆曲线连接处，它的半径等于圆曲线的半径R。同样，随着半径的逐渐减小，使相应的超高和加宽之间增大，起到过渡的作用，这种曲率半径处处都在改变的曲线称为缓和曲线。

缓和曲线可用多种曲线来代替，如回旋线、三次抛物线和双曲线等。我国公路部门一般都采用回旋线作为缓和曲线。从直线段连接处起，缓和曲线上各点的曲率半径ρ和该点离缓和曲线起点的距离l成反比。即：

C是一个常数，称为缓和曲线变更率。在与圆曲线连接处，l等于缓和曲线全长l0，ρ等于圆曲线的半径R，故：

C＝R·l0　(13-8)

C一经确定，缓和曲线的形状也就确定。C愈小，半径的变化愈快；反之，C愈大，半径的变化愈慢，曲线也就愈平顺。当C为定值时，缓和曲线的长度视所连接的圆曲线半径而定（见图13-7）。

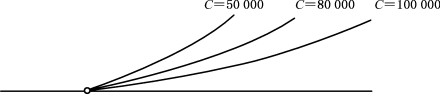
图13-7　缓和曲线

2）缓和曲线方程式

由上述可知，缓和曲线是按线性规则变化的，其任意点的半径为：

在图13-8中：(www.daowen.com)

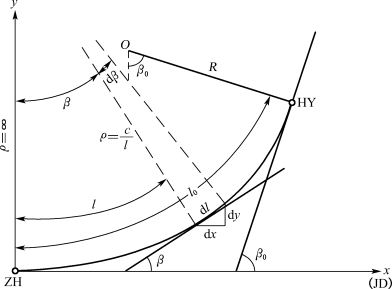
图13-8　缓和曲线方程式

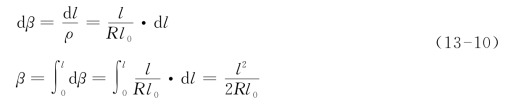
当l＝l0时，

即相当于圆曲线弧长l0所对的圆心角的一半。由图13-8中又可得出：

dx＝dl·cosβ

dy＝dl·sinβ

将sinβ和cosβ用泰勒级数展开得：

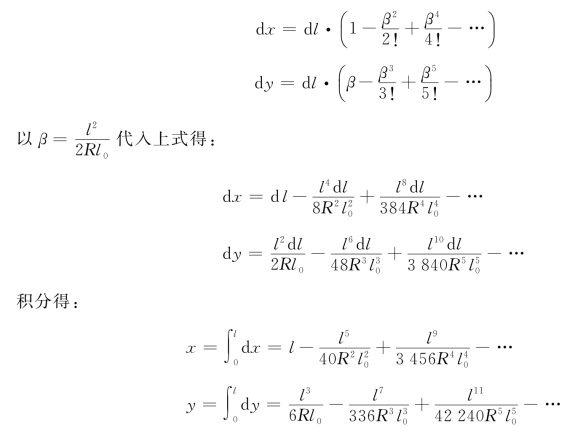
上式中高次项略去，便得出曲率按线性规则变化的缓和曲线方程式为：

缓和曲线终点的坐标为（取l＝l0）：