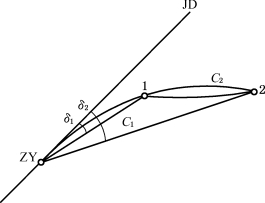
图13-5　偏角法测设圆曲线

在测设曲线控制点的基础上，详细测设圆曲线的细部中桩点称为曲线的细部放样。常用的传统方法是偏角法。所谓偏角法，就是将经纬仪安置在曲线上任意一点（通常是曲线控制点），则曲线上所欲测设的各点可用相应的偏角δ和弦长C1来测定。偏角是指安置经纬仪的测站点的切线和待定点的弦之间的夹角，即弦切角。如图13-5中，ZY为测站点，以切线方向为零方向，第一点可用偏角δ1和1点至ZY点的弦长C1来测设，第二点可用偏角δ2和从1点量至2点的弦长C2来测设。以后各点均可用同样的方法测设。即用偏角来确定测设点的方向，而距离是从相应点上量出弦长而得到。该方法实际上是方向和距离交会法。由此可见，用偏角法测设圆曲线必须先计算出偏角δ和弦长C。

偏角δ即弦切角，它等于相应弦所对圆心角之半：

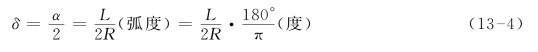
式中：R——曲线的半径；

L——测站点到测设点的弧长。

由式（13-4）可知，对于半径R确定的圆曲线，偏角与弧长成正比。当弧长成倍增加时，相应的偏角也成倍增加；当弧长增加某一固定值时，偏角也相应增加一固定角值。这就是圆曲线上偏角的特性。

如图13-5中，ZY点至1点的弧长l1可通过两点里程求得，偏角δ1为：

而从第1点开始，通常都是弧长增加相等的值l0，则可以先求点l0所对应的偏角δ0：(www.daowen.com)

以后每增加弧长l0，偏角就增加一个δ0，即：

δ2＝δ1＋δ0

δ3＝δ1＋2δ0

⋮

δi＝δ1＋(i-1)·δ0

弦长的计算公式为：

C＝2R·sinδ

在实际操作中，用经纬仪拨偏角时，存在正拨和反拨的问题。当相邻为右转向时，偏角为顺时针方向，以切线方向为零方向时，经纬仪所拨角即为偏角值，此时为正拨；当线路为左转向时，偏角为逆时针方向，经纬仪所拨角应为360°-δ，此时为反拨。

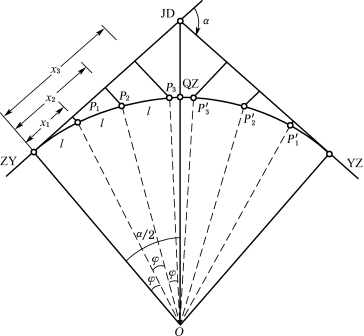
图13-6　切线支距法测设圆曲线