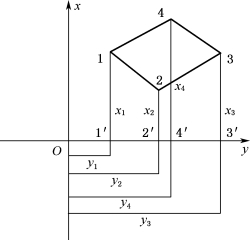
图10-8　坐标解析法

在规划设计中，往往需要测定某一地区或某一图形的面积。例如，林场面积、农田水利灌溉面积调查，土地面积规划，工业厂区面积计算等。

设图上面积为P图，则：

P实＝P图×M2　（10-9）

式中：P实——实地面积；

M——比例尺分母。

设图上面积为10mm2，比例尺为1∶2000，则实地面积P实＝10×20002÷106＝40m2。(www.daowen.com)

若待测图形为多边形，可根据多边形各个顶点的坐标用坐标解析法计算面积。由图10-8可知：多边形1234的面积等于梯形144′1′面积P144′1′加梯形433′4′面积减梯形233′2′面积P233′2′减梯形122′1′面积P122′1′，即：

P＝P144′1′＋P433′4′-P233′2′-P122′1′

设多边形顶点1、2、3、4的坐标分别为（x1、y1）、（x2、y2）、（x3、y3）、（x4、y4）。将上式中各梯形面积用坐标值表示，即：

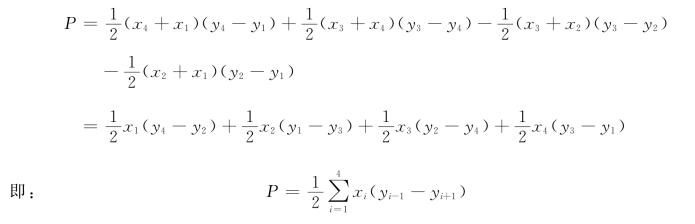
同理，可推导出n边形面积的坐标解析法计算公式为：

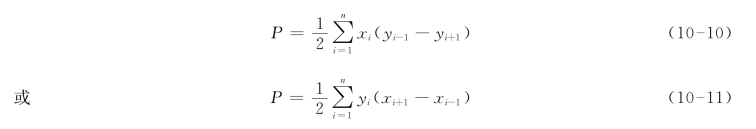
注意式中当i＝1时，令i-1＝n；当i＝n时，令i＋1＝1。

应利用式（10-9）和式（10-10）计算同一图形面积，检核计算的正确性。采用以上两式计算多边形面积时，顶点1、2、3、…、n应按逆时针方向编号。若把顶点依顺时针编号，按上两式计算，面积计算值不变，仅符号相反。