自由测站是一种较新颖的测量方法,以一测站为一坐标系(称“测站坐标系”或“局部坐标”),不同的观测站具有不同的测站坐标系,最后将各测站坐标系转换至相同之坐标系(称“全区坐标系”或“全域坐标系”),故施测时可以任意点为测站,任意方向为北方,观测的是测站附近各点以测站坐标系为基准之坐标值。
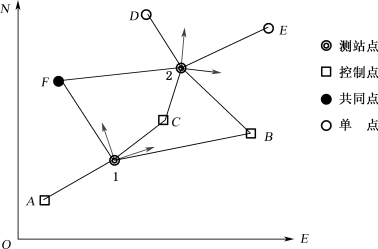
图8-20 自由设站原理图
1)基本原理
定义自由测站法各种点的关系如下:
(1)测站点:整置仪器之点。
(2)共同点:为了使全区有统一坐标,故部分的点位须被两个或多个测站所观测,以求得各测站之转换关系,此种被两个以上之测站所观测之点称为共同点。
(3)控制点:已知全区坐标之点称为控制点。若欲以已知坐标系为全区坐标系,则部分测站须观测控制点。
(4)单点:即非控制点,且仅被某一测站所观测,则称为单点(Single Point)。通常为地物或地形要点。
图8-20中有2个测站点,3个控制点(A,B,C),1个共同点(F)及2个单点(D,E),以自由测站法施测后可得二个不同测站坐标系,经坐标转化后可得全区坐标系。
2)自由测站优点
(1)施测时
①可以任意点设置站,不需置于控制点,故可在欲测区域附近设测站,方便细部测量实施。
②可以任意方向为北方,可免除对点定方位之操作,故测站与测站间不需互相通视。
③控制点不需先行检测。
④控制测量与细部测量可同时施测。(www.daowen.com)
(2)平差时
①观测值即为平差程式之输入值,不需寻找各测站或观测量之关系,故观测值不需再加整理。若使用具有自动记录功能之全站仪,则可直接输入自由测站法之平差程式,而避免人为之错误。
②不需先行计算各点之近似坐标。
③不需计算投影改正。
③全区平差解算,点位精度甚为均匀。
3)自由测站之计算
如果有2个以上点既具有全区坐标(Xg,Yg),又具有测站坐标(xl,yl),且测站坐标原点相对于全区坐标为(Xg/l,Yg/l),则可利用「坐标转换」将所有测点的测站坐标转换成全区坐标,其坐标转换如下:
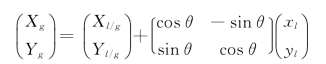
由A、B两个点位代入可得:
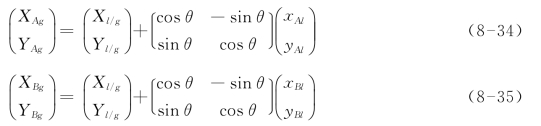
以上两式相减,得下式:
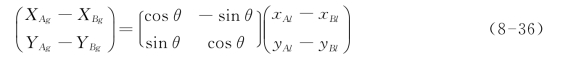
由式(8-34)可以得:
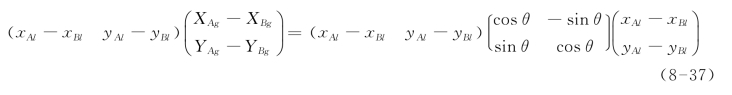
可得:
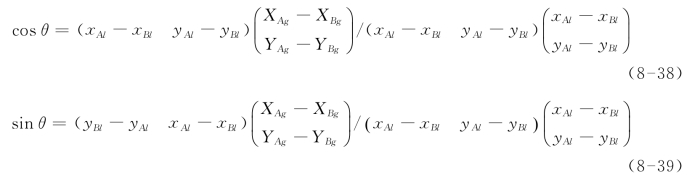
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






