如图8-14，在三角形ABP中已知点A、B的坐标为xA、yA和xB、yB。在A、B两点设站，测得α、β两角，即可按坐标正算公式求得P点的坐标，即：

xP＝xA＋SAPcosαAP

yP＝yA＋SAPsinαAP

考虑到αAP＝αAB-α，并由：

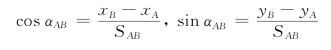
可得：

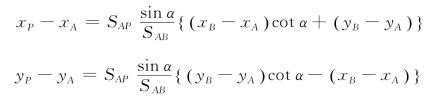
由正弦定理得：

则：

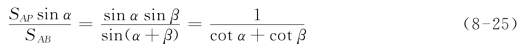
因此有：

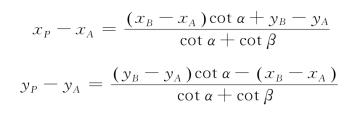(www.daowen.com)

移项化简即得：

上式称为余切公式（或变形的戎格公式）。

必须指出：

（1）在一般测量规范中，都要求布设有3个起始点的前方交会（见图8-16）。这时在A、B、C3个已知点向P点观测，测出了4个角值：α1、β1、α2、β2，分两组计算P点坐标。计算时可按△ABP求P点坐标再按△BCP求P点坐标当这两组坐标的较差在容许限差内，则取它们的平均值作为P点的最后坐标。在一般测量规范中，对于地形控制点，上述限差是这样规定的：要求两组算得的点位较差不大于两倍比例尺精度，用公式表示为：

式中

M——测图比例尺分母。

（2）在测角交会的图形中，由未知点至相邻两起始点间方向的夹角称为交会角。当交会角过小（或过大）时，由于A和B角含有误差Δα和Δβ，将使P点有较大的位移PP′（见图8-17）。所以要求交会角一般应大于30°并小于150°。

图8-16　三边前方交会

举例说明：为了求得地形控制点P（图8-16）的坐标，分别在已知点A、B、C设站观测了四个角，试按前方交会计算P点坐标。

在△ABP中∠PAB＝α1，∠ABP＝β1；在△BCP中∠PBC＝α2，∠BCP＝β2。按式（8-25）求得P点的两组坐标：16226.42m。所以Δx＝0.03m，Δy＝0.00m，则＝0.03m。设M＝10000，则2×0.1M（mm）＝2m，由于ΔS＜2×0.1M（mm），故取两组坐标的平均值作为P点的最或然坐标，xP＝37194.56m，yP＝16226.42m。