1）概述

经纬仪导线在野外施测完毕后，即可进行内业计算。计算前应该先做以下工作：

（1）整理和检查导线测量的记录。

（2）将倾斜改正数加到导线边的实测长度上，得出导线边的最后边长。

（3）将已知数据和整理好的测量成果填入坐标计算表中。

（4）根据导线边长和角度按比例绘制导线略图。

这些成果整理工作很重要，应予以重视。

2）内业计算步骤

经纬仪导线计算的目的是求得各导线点的坐标，并根据求得的各点坐标精确地绘制导线图。导线计算一般可分为以下五个步骤进行：①角度闭合差的计算和调整；②坐标方位角的推算；③坐标增量的计算；④坐标增量闭合差的计算和调整；⑤计算各导线点的坐标。

3）闭合导线的计算

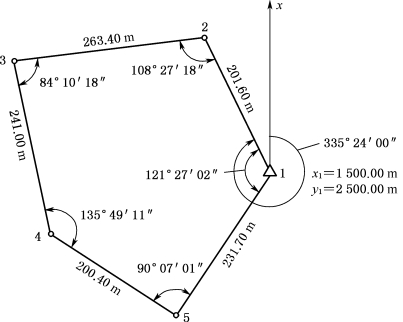
图8-11　闭合导线略图

现以图8-11所注的数据为例，结合“闭合导线坐标计算表”的使用，说明闭合导线坐标计算的步骤。

（1）角度闭合差的计算与调整

①计算角度闭合差

如图8-11所示，n边形闭合导线内角和的理论值为：

∑β理＝（n-2）×180°　（8-8）

式中：n——导线边数或转折角数。

由于观测水平角不可避免地含有误差，致使实测的内角之和∑β测不等于理论值∑β理，两者之差，称为角度闭合差，用fβ表示，即：

fβ＝∑β测-∑β理＝∑β测-（n-2）×180°　（8-9）

②计算角度闭合差的容许值

角度闭合差的大小反映了水平角观测的质量。导线计算中的闭合差是由于观测值中存在误差而产生的，因此闭合差的大小将反映出观测值的误差大小。如果闭合差过大，则表明观测值中的误差太大。为了限制观测值的误差值，在导线计算中常对闭合差给以一个容许值，通常称为限差。

各级导线角度闭合差的容许值fβ见表8-2，其中图根导线角度闭合差的容许值fβ限的计算公式为：

如果|fβ|＞|fβ限|，说明所测水平角不符合要求，应对水平角重新检查或重测。

如果fβ≤|fβ限|，说明所测水平角符合要求，可对所测水平角进行调整。

③计算水平角改正数

如角度闭合差不超过角度闭合差的容许值，则将角度闭合差反符号平均分配到各观测水平角中，也就是每个水平角加相同的改正数vβ。vβ的计算公式为：

当fβ不能被n整除时，在有效数字位内允许凑整。

计算检核：水平角改正数之和应与角度闭合差大小相等符号相反，即：

∑vβ＝-fβ

④计算改正后的水平角

改正后的水平角βi改等于所测水平角加上水平角改正数：

βi改＝βi＋vβ　（8-12）

计算检核：改正后的闭合导线内角之和应为（n-2）×180°，本例为540°。

本例中fβ、fβ限的计算见表8-4辅助计算栏，水平角的改正数和改正后的水平角见表8-4第2栏。

（2）推算各边的坐标方位角

根据起始边的已知坐标方位角及改正后的水平角，按式（8-2）和式（8-3）推算其他各导线边的坐标方位角。

本例观测左角，按式（8-2）推算出导线各边的坐标方位角，填入表8-4的第4栏内。

计算检核：最后推算出起始边坐标方位角，它应与原有的起始边已知坐标方位角相等，否则应重新检查计算。

（3）坐标增量的计算

根据已推算出的导线各边的坐标方位角和相应边的边长，按坐标正算公式即式（8-4）计算各边的坐标增量。例如，导线边1～2的坐标增量为：

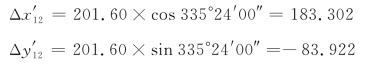
用同样的方法，计算出其他各边的坐标增量值，填入表8-4的第6、7两栏的相应格内。

（4）坐标增量闭合差的计算和调整

①计算坐标增量闭合差

如图8-12（a）所示，闭合导线，纵、横坐标增量代数和的理论值应为零，即：

图8-12　坐标增量闭合差

实际上由于导线边长测量误差和角度闭合差调整后的残余误差，使得实际计算所得的∑Δx测、∑Δy测不等于零，从而产生纵坐标增量闭合差fx和横坐标增量闭合差fy，即：

②计算导线全长闭合差fD和导线全长相对闭合差fk

从图8-12（b）可以看出，由于坐标增量闭合差fx、fy的存在，使导线不能闭合，1-1′之长度fD称为导线全长闭合差，并用下式计算：

仅从fD值的大小还不能说明导线测量的精度，衡量导线测量的精度还应该考虑到导线的总长。将fD与导线全长∑D相比，以分子为1的分数表示，称为导线全长相对闭合差fk，即：

以导线全长相对闭合差fk来衡量导线测量的精度，fk的分母越大，精度越高。不同等级的导线，其导线全长相对闭合差的容许fk限值参见表8-2，图根导线的fk限为1/2000。

如果fk＞fk限，说明成果不合格，此时应对导线的内业计算和外业工作进行检查，必要时须重测。

如果fk≤fk限，说明测量成果符合精度要求，可以进行调整。(www.daowen.com)

本例中fx、fy、fD及fk的计算见表8-4辅助计算栏。

③调整坐标增量闭合差

调整的原则是将fx、fy反号，并按与边长成正比的原则，分配到各边对应的纵、横坐标增量中去。以vxi、vyi分别表示第i边的纵、横坐标增量改正数，即：

本例中导线边1～2的坐标增量改正数为：vx12＝＋0.010，vy12＝-0.013

用同样的方法，计算出其他各导线边的纵、横坐标增量改正数，填入表8-4的第6、7栏坐标增量值相应方格的上方。

计算检核：纵、横坐标增量改正数之和应满足下式：

④计算改正后的坐标增量

各边坐标增量计算值加上相应的改正数，即得各边的改正后的坐标增量。

本例中导线边1～2改正后的坐标增量为：

Δx12＝183.302＋(＋0.010)＝180.312

Δy12＝-83.922＋(-0.013)＝-83.935

用同样的方法，计算出其他各导线边改正后坐标增量，填入表8-4的第8、9栏内。

计算检核：改正后纵、横坐标增量之代数和应分别为零。

（5）计算各导线点的坐标

根据起始点1的已知坐标和改正后各导线边的坐标增量，按下式依次推算出各导线点的坐标：

将推算出的各导线点坐标，填入表8-4中的第10、11栏内。

最后还应再次推算起始点1的坐标，其值应与原有的已知值相等，以作为计算检核。

以上整个计算过程见表8-4。

4）附合导线的计算

附合导线的坐标计算与闭合导线的坐标计算步骤和方法基本相同，只是在计算角度闭合差与计算坐标增量闭合差的公式稍有差别。

（1）角度闭合差的计算与调整

①角度闭合差的计算

附合导线的角度闭合差为从一已知边方位角出发，使用观测角推算另一条已知边，推算方位角和已知方位角之差。如图8-13所示，根据起始边AB的坐标方位角αAB及观测的各右角，按式（8-3）推算CD边的坐标方位角αCD。

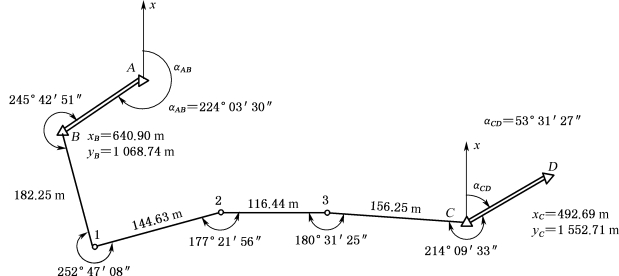
图8-13　附合导线略图

αB1＝αAB＋180°-βB

α12＝αB1＋180°-β1

α23＝α12＋180°-β2

α3C＝α23＋180°-β3

αCD＝α3C＋180°-βC

将上式相加，得：

αCD＝αAB＋5×180°-∑β右

写成一般公式，右角观测值之理论值应满足：

若观测左角，则左角观测值之理论值应满足：

附合导线的角度闭合差fβ为：

fβ＝∑β测-∑β理　（8-23）

②调整角度闭合差

当角度闭合差在容许范围内，则将角度闭合差反号平均分配到各角。

（2）坐标方位角的推算

根据起始边的已知坐标方位角及改正后的水平角，按式（8-2）和式（8-3）推算其他各导线边的坐标方位角。

（3）坐标增量的计算

根据导线各边的方位角和边长，计算各坐标增量，计算方法和闭合导线相同。

（4）坐标增量闭合差的计算与分配

因为附合导线的起点与终点不一致，所以理论上的纵横坐标增量之和不等于零，而是等于两端已知点的纵横坐标之差，即：

∑Δx理＝x终-x始

∑Δy理＝y终-y始

表8-4　闭合导线解算表

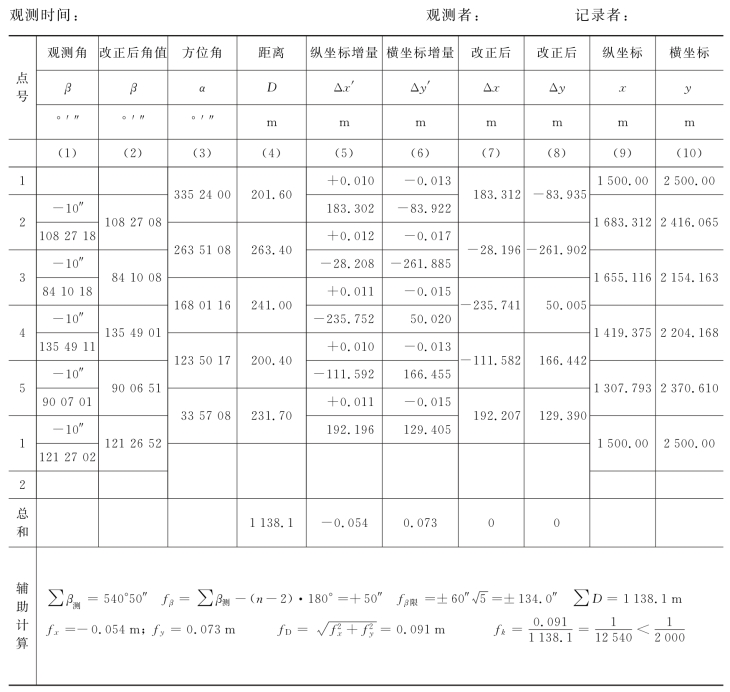
由于测角和量边都存在误差，计算得到的纵横坐标增量的总和∑Δx测、∑Δy测与其理论值不一致，而是产生坐标增量闭合差fx、fy，即：

fx＝∑Δx测-∑Δx理＝∑Δx测-（x终-x始）

fy＝∑Δy测-∑Δy理＝∑Δy测-（y终-y始）

（5）坐标的计算

坐标增量闭合差分配以后，根据导线一端的高级控制点的坐标，以及改正后的坐标增量，按照导线坐标计算的方法，逐点计算各导线点的坐标。最后算出的另一端的高级控制点的坐标，应与其已知值相同，以此作为检核。整个附合导线的计算过程参见表8-5。

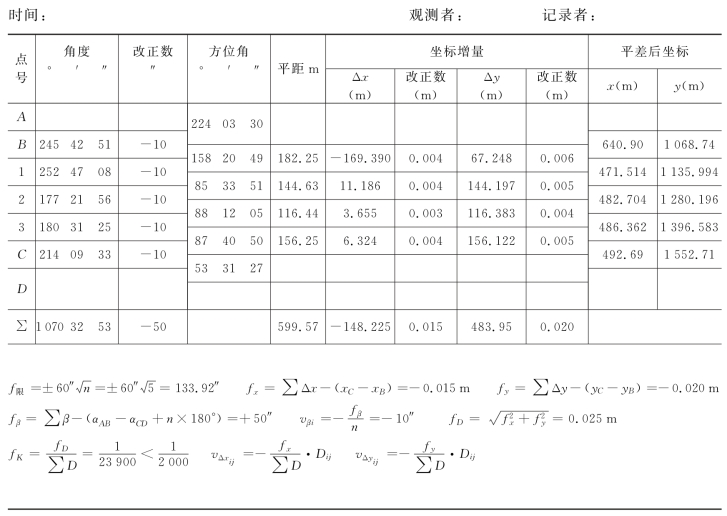
表8-5　附合导线解算表