1）函数中误差的计算方法

设Z是一组独立的直接观测值x1，x2，…，xn的函数，即z＝f（x1，x2，…，xn），各直接观测值对应的真误差分别为Δ1，Δ2，…，Δn，对该函数进行全微分并按泰勒级数展开，则有：

当xi具有真误差Δi时，函数Z则产生相应的真误差Δz。因为真误差Δ是一微小量，所以可用真误差来代替式（7-9）中的dz，dx1，dx2，…，dxn，得到：

式中：是函数对xi取的偏导数并用观测值代入算出的数值，它们是常数。因此，上式变成了线性函数。

对于微小量Δ，其正、负符号出现的机会相同，它们之间的乘积之和趋近于0，式（7-10）可改写为：

用中误差m代替真误差Δ，代入上式，整理得到函数中误差计算公式：

【例7-2】　丈量得到某一段斜距S＝106.28m，测得斜距的竖直角δ＝8°30′，已知中误差ms＝±5cm、mδ＝±20″，求改算后的平距的中误差mD。

【解】

D＝S·cosδ

全微分化成线性函数，用“Δ”代替“d”，得：

ΔD＝cosδ·Δs-SsinδΔδ

应用式（7-12）后，得：

注意：在上式计算中将单位统一为厘米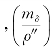是将角值的单位由秒化为弧度。

2）特殊函数中误差的计算方法

（1）倍数函数

设有函数

z＝kx　(7-13)

式中：k为常数，x为直接观测值，其中误差为mx，求观测值函数z的中误差mz。

该函数的全微分dz＝kdx，由式（7-12）可求得：

mz＝±kmx　(7-14)

即观测值倍数函数的中误差，等于观测值中误差乘倍数（常数）。(www.daowen.com)

【例7-3】　用视距测量方法测量AB距离，已知视线水平，观测视距间隔的中误差ml＝±1cm，k＝100，求平距的中误差mD。

【解】　水平视距公式

D＝k·l

则平距的中误差

mD＝100·ml＝±1m。

（2）和差函数

设有函数

z＝x±y　(7-15)

式中：x、y为独立的直接观测值，对应的中误差分别为mx和my，求观测值函数Z的中误差mz。该函数的全微分dz＝dx±dy，由式（7-12）可求得：

即观测值和差函数的中误差等于两观测值中误差的平方之和的平方根。

【例7-4】　对△ABC观测了A、B两个角，测角中误差分别为mA＝±3″，mB＝±4″，求按公式∠C＝180°-∠A-∠B计算得到的第三个角的中误差mC。

【解】　对于公式∠C＝180°-∠A-∠B，则∠C的中误差

（3）线性函数

设有线性函数

z＝k1x1±k2x2±…±knxn　(7-17)

式中：x1，x2，…，xn为独立的直接观测值，对应的中误差分别为mx1，mx2，…，mxn，k1，k2，…，kn为常数，则综合式（7-14）和式（7-16）可得：

【例7-5】　有一函数z＝2x1＋x2＋3x3，其中x1、x2、x3为独立的直接观测值，其对应的中误差分别为±3mm、±2mm、±1mm，求函数z的中误差mz。

【解】　由已知得dz＝2dx1＋dx2＋3dx3，则mz＝±＝±7mm。

应用误差传播定律求观测值的中误差时，首先要按要求写出函数式，函数式中的各个观测值应相互独立；再对函数式进行全微分，求出函数与观测值真误差的关系式，再按式（7-12）计算结果。对于倍数函数、和差函数、线性函数则分别按式（7-14）、式（7-16）、式（7-18）求解。