概率论中衡量观测值精度的指标是观测误差的标准差σ，其表达式为：

式中：其他符号含义同前。

由此可见标准差是依据无穷多个观测值计算出的理论上的观测精度，而在测量实践中对某量的等精度观测总是有限次的，这样就只能以有限的观测次数n计算出标准差的估值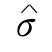，并将标准差的估值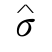定义为中误差m，作为衡量测量结果精度的一种标准，计算公式为：

使用中误差评定观测值精度时，应注意：

（1）在一组同精度的观测值中，尽管各观测值的真误差Δ出现的大小和符号各异，但每个观测值的中误差却是相同的，因为中误差反映观测的精度，只要观测条件相同，则中误差不变。

（2）中误差代表的是一组观测值的误差分布，它是根据统计学原理来衡量观测值精度的，所以观测值个数不能太少，否则会失去可靠性。(www.daowen.com)

（3）中误差数值前应有“±”号，因为中误差所表示的精度是误差的某个区间。

【例7-1】　甲、乙两组各自在相同的观测条件下测量了六个三角形的内角，得到三角形的闭合差（即三角形内角和的真误差）分别为：

甲组：＋3″、＋1″、-2″、-1″、0″、-3″；乙组：＋6″、-5″、＋1″、-4″、-3″、＋5″。试分析两组的观测精度。

【解】　依据式（7-4）计算得两组观测值中误差分别为：

从上述两组结果中可以看出，因为m甲＜m乙，所以甲组观测精度高于乙组。显然这是由于甲组观测误差的离散程度小于乙组所致。正是由于中误差能反映绝对值较大的观测误差的影响，因而在测量工作中普遍采用中误差来评定测量成果的精度。