测量工作的基准面——大地水准面是一个极其复杂的曲面，测量数据要归化计算（投影）到该曲面上是很困难的，因此，我们已将其简化为圆球面。

在普通测量范围内，将地面点投影到该圆球面上，然后再投影到平面图纸上描绘，显然这还是很复杂的工作。在实际测量工作中，在一定的精度要求和测量面积不大的情况下，往往以水平面代替水准面，即把较小一部分地球表面上的点投影到水平面上来决定其位置，这样可以简化计算和绘图工作。

从理论上讲，将极小部分的水准面（曲面）当作水平面也是要产生变形的，必然对测量观测值（如距离、高差等）带来影响。当上述这种影响较小，不超过规定的误差范围时，认为用水平面代替水准面是可以的，而且是合理的。本节主要讨论用水平面代替水准面对距离和高差的影响（或称地球曲率的影响），以便给出水平面代替水准面的限度。

1）地球曲率对距离的影响

图1-8　地球曲率的影响

如图1-8所示，设球面（水准面）P与水平面P′在A点相切，A、B两点在球面上弧长为D，在水平面上的距离（水平距离）为D′，即：

D＝R·θ

D′＝R·tanθ

式中：R——球面P的半径；

θ——弧长D所对角度。

以水平面上距离D′代替球面上弧长D所产生的误差为ΔD，则：

ΔD＝D′-D＝R(tanθ-θ)　(1-2)

将式（1-2）中tanθ按级数展开，并略去高次项，得：

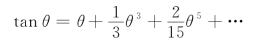
将上式代入式（1-2），并顾及整理可得：

若取地球平均曲率半径R＝6371km，并以不同的D值代入式（1-3）或式（1-4），则可得出距离误差ΔD和相应相对误差ΔD/D，如表1-1所列。

表1-1　水平面代替水准面的距离误差和相对误差

(www.daowen.com)

由表1-1可知，当距离为10km时，用水平面代替水准面（球面）所产生的距离相对误差为1/1220000，这样小的距离误差就是在地面上进行最精密的距离测量也是允许的。因此，可以认为在半径为10km的范围内（相当面积320km2），用水平面代替水准面所产生的距离误差可忽略不计，也就是可不考虑地球曲率对距离的影响。当精度要求较低时，还可以将测量范围的半径扩大到25km（相当面积2000km2）。

2）地球曲率对水平角的影响

由球面三角学可知，同一个空间多边形在球面上投影的各内角之和，较其在平面上投影的各内角之和要大一个球面角超ε，它的大小与图形面积成正比。其计算公式为：

式中：P——球面多边形面积；

R——地球半径；

ρ″——1弧度所对应的秒角值（ρ″＝206265″）。当P＝100km2时，ε＝0.51″。

通过计算可知，对于面积在100km2内的多边形，地球曲率对水平角的影响值ε是很小的。因此，对于地球曲率对水平角的影响，只有在精密测量中才会考虑，而一般测量工作是可以忽略不计的。

3）地球曲率对高差的影响

在图1-8中，A、B两点在同一球面（水准面）上，其高程应相等（即高差为零）。B点投影到水平面上得B′点。则BB′即为水平面代替水准面产生的高差误差。设BB′＝Δh，则

(R＋Δh)2＝R2＋D′2

整理得：

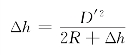
上式中，可以用D代替D′，同时Δh与2R相比可略去不计，则

以不同的D代入式（1-6），取R＝6371km，则得相应的高差误差值，如表1-2所列。

表1-2　水平面代替水准面的高差误差

由表1-2可知，用水平面代替水准面，在1km的距离上高差误差就有78mm，即使距离为0.1km（100m）时，高差误差也有0.8mm。所以，在进行水准测量时，即使很短的距离都应考虑地球曲率对高差的影响。