在本书5.4节讨论的软弱薄夹层破坏问题中，由于夹层厚度很薄，夹层可近似看为一弱面，破坏的方式为滑移失稳，其中忽略了夹层厚度以及夹层本身材料力学特性的影响。如本书5.1节所述，在盐岩溶腔顶板中通常还存在较厚夹层，夹层厚度的影响无法忽略，这将直接导致问题更为复杂。夹层与盐岩交界面可能的破坏方式除了沿界面的滑移失稳，还可能发生界面处夹层与盐岩本身的强度破坏。

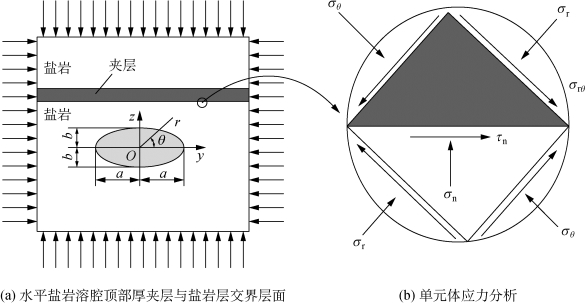
界面应力的求解仍然是建立界面失稳条件的关键。与上节的分析方法相同，首先建立顶部厚夹层与盐岩层交界层面的力学模型，如图5-31所示，其夹层界面单元体应力分析如图5-31（b）所示。由于图5-31（b）所取单元体为各向异性，此时界面应力σn，τn的求解与上节相比变得极其复杂，界面上、下分别为盐岩与夹层，单元体上部的应力σθ，σr与下部的应力σθ，σr不再相等，该问题属于数学弹性力学中的第一类基本问题，不能单纯将其简化为平面小孔应力集中。早在20世纪30年代，穆斯海里什维里[95]、路见可[96]等就进行了深入的研究，由于数学上的求解困难，截至目前，该问题仍未得到有效解决。目前只能通过复变函数理论获得一些较简单问题（单个夹层）的结果[97]，无法直接应用到工程实际计算中。关于夹层厚度、夹层数量、夹层位置等一些关键因素对夹层界面失稳的影响，只能通过数值方法进行计算。

(www.daowen.com)

图5-31　水平盐岩溶腔顶部厚夹层与盐岩层交界层面及应力分析示意图

在界面应力分析结果的基础上，对于夹层与盐岩交界面沿界面的滑移失稳主要取决于界面上的正应力σn和切应力τn，属于单剪的情况，因此其滑移失稳条件仍然可采用Mohr-Coulom准则；而对于界面处夹层和盐岩本身发生的强度破坏，非线性三剪能量屈服准则比Mohr-Coulom准则理论更加全面、准确，所得极限应力更加符合盐岩以及夹层材料的实际情况，因此在本节后续计算中，采用非线性三剪能量屈服准则作为破坏判据。