绝大多数岩石的主要破坏形式为剪切破坏，岩石体积改变对其剪切破坏形式的强度几乎没有影响，因此予以忽略；岩石材料的破坏主要由其剪切变形的大小所控制。

如图5-2（b）所示，对于岩石材料，通常会在切应力与法向正应力比值（τ/σ）最大的作用面上发生破坏。当σ1≥σ2≥σ3时，则有φ13≥φ12，φ13≥φ23。设φ13=φ，c 13=c。在最大内摩擦角φ13作用面上的剪切应变能可表示为

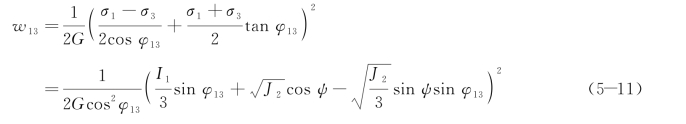
式中J 2——第二应力偏量不变量；

I 1——第一应力不变量；

φ——最大内摩擦角；

ψ——洛德角；

c——内聚力。

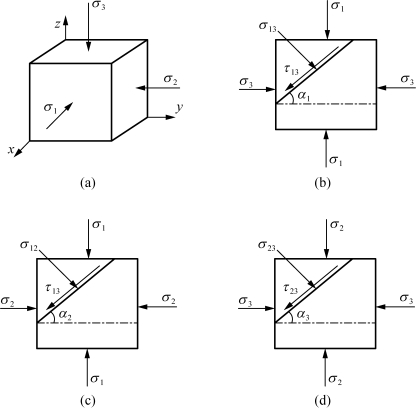
图5-2　单元体剪切破坏示意图

若认为当w 13达到某一极限值时，即发生屈服，那么单剪能量屈服准则可表示为

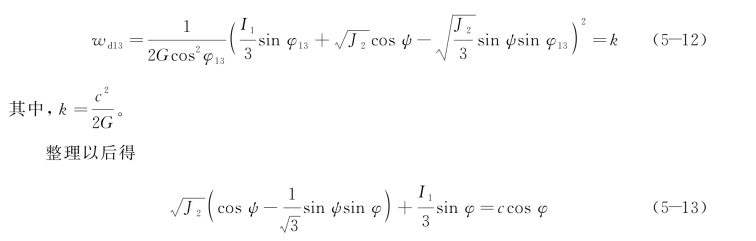
可以看出，式（5-13）即为用应力不变量及应力偏量不变量表示的Mohr-Coulom屈服准则，如前所述，式（5-13）仅仅考虑了一个剪切面上的破坏，只包含了最大、最小主应力的影响，没有考虑中间主应力。

若考虑三向应力状态，即存在三个破坏面，如图5-2（b）—（d）所示。三个破坏面与主应力的夹角α1，α2，α3分别为根据Mohr圆几何关系，即可解出三个面的正应力和切应力，同时再考虑各个面上摩擦应力的影响，则三个面上的剪切应变能的极限值可写为

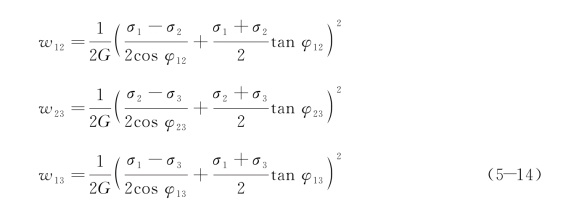(www.daowen.com)

式中，G为剪切弹性模量。

三剪能量屈服准则认为：当三个最大摩擦角作用面的剪切应变能之和达到某个值时，岩石发生屈服。因此，可将其表示为

k值可由常规三轴试验结果获取：

将式（5-14）、式（5-16）代入式（5-15），并用应力不变表示为

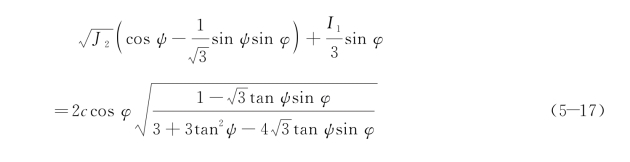
线性三剪能量屈服准则的具体表达式即为式（5-17）。可以看出，三剪能量屈服准则与Mohr-Coulom屈服准则有着相似的表达式，式（5-17）与式（5-13）的左边完全相同，只是式（5-17）右边比式（5-13）多了一个与洛德角ψ有关的常数项。

如图5-3所示，与Mohr-Coulom准则相比，在主应力空间中，三剪能量屈服面变成了一个曲线形椎体面；并且可以看出，平均应力σm对岩石材料的屈服产生直接影响，屈服面在π平面上的迹线所包含的范围随σm不同而不同。

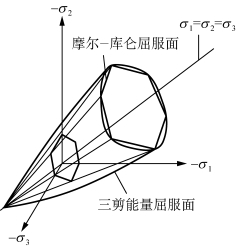
图5-3　三剪能量屈服面示意图

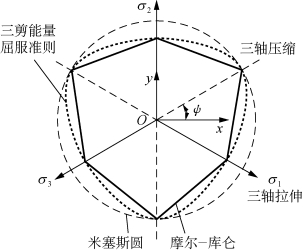
图5-4　三剪能量屈服面在π平面的迹线示意图

图5-4给出了线性三剪能量屈服准则在任一π平面的迹线，可以看出：在π平面上，线性三剪能量屈服准则实质上是外接于Mohr-Coulom屈服准则的一个曲边三角形，因此，Mohr-Coulom准则比其略保守；在ψ=-30°或ψ=30°处，三剪能量屈服准则与Mohr-Coulom准则一致；且在ψ=30°处，岩石强度最高（三轴压缩状态），在ψ=-30°处，岩石强度最小（三轴拉伸状态）。线性三剪能量屈服准则补充了屈服强度在π平面随洛德角ψ的非线性变化关系，这一点与大多数岩石的试验结果相符。