在画法几何中，直线由直线上任意两个点的位置确定，因此直线的投影可由直线上两点的投影来确定，将直线上点的投影相连，即得到直线在该投影面上的投影。

（一）直线的三面投影

空间一直线的投影可由直线上的两点（通常取线段两个端点）的同面投影来确定。如图2-21（a）所示的直线AB，求作它的三面投影图时，如图2-21（b）所示可分别作出A、B两端点的投影（a，a′，a″）、（b，b′，b″），然后将其同面投影连接起来即得直线AB的三面投影图，如图2-21（c）所示。

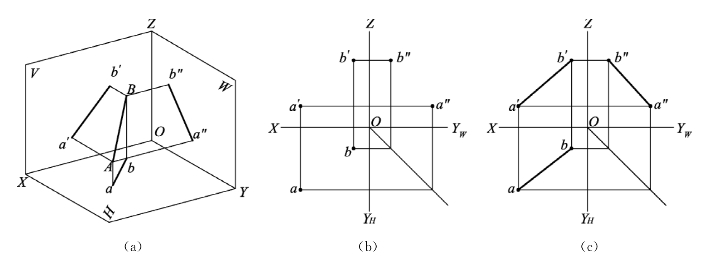
图2-21　直线的三面投影

（二）直线的投影规律

根据与投影面的相对位置，直线可分为一般位置直线和特殊位置直线。特殊位置直线分为投影面的平行线（水平线、正平线、侧平线）和投影面的垂直线（铅垂线、正垂线、侧垂线）。

1.投影面的平行线

只平行于一个投影面，倾斜于另外两个投影面的直线，称为某投影面的平行线。

（1）平行于V面而倾斜于H、W面的直线，称为正平线（表2-1a）。

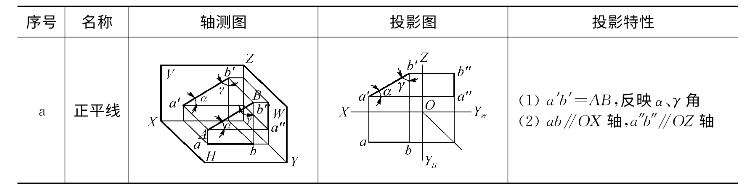
（2）平行于H面而倾斜于V、W面的直线，称为水平线（表2-1b）。

（3）平行于W面而倾斜于V、H面的直线，称为侧平线（表2-1c）。

表2-1　投影面平行线的投影特性

（续表）

2.投影面的垂直线

垂直于一个投影面，而平行于另外两个投影面的直线，称为某投影面的垂直线。

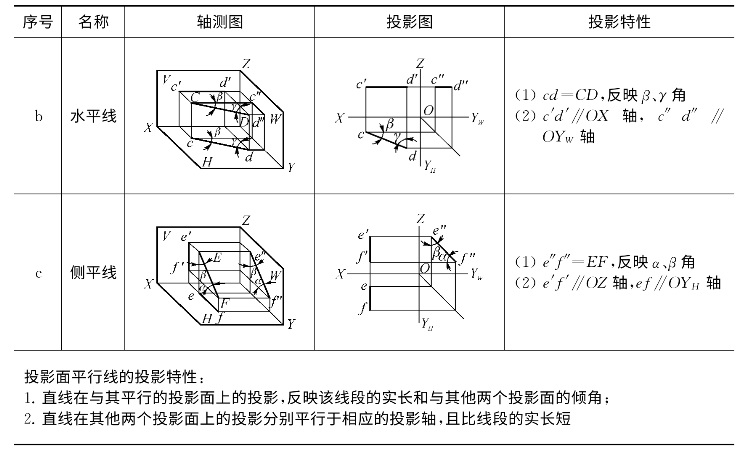
（1）垂直于V面、平行于H、W面的直线，称为正垂线（表2-2a）。

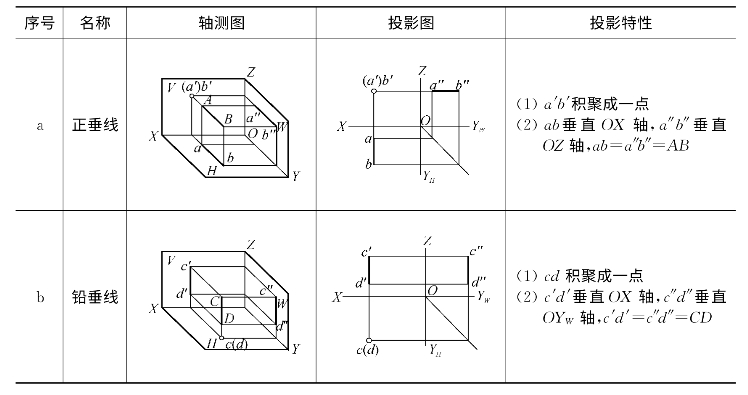
（2）垂直于H面、平行于V、W面的直线，称为铅垂线（表2-2b）。

（3）垂直于W面、平行于V、H面的直线，称为侧垂线（表2-2c）。

表2-2　投影面垂直线的投影特性

（续表）

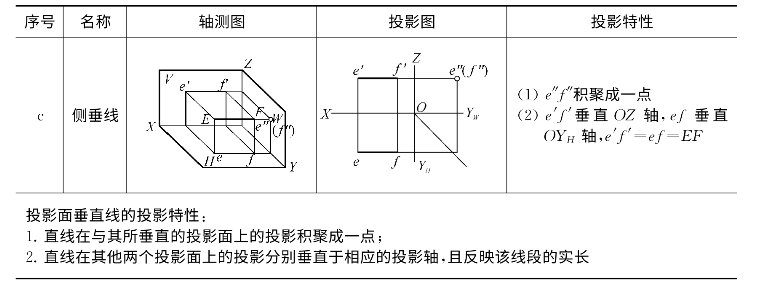
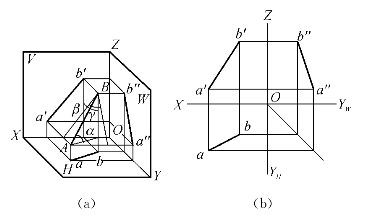
图2-22　一般位置直线

3.一般位置直线

倾斜于三个投影面的直线，称为一般位置直线，也可称为倾斜线。图2-22（a）为一般位置直线的直观图，直线与它在某一投影面上的投影所形成的锐角，称为直线对该投影面的倾角。直线对H、V、W面的倾角分别用α、β、γ表示。从图2-22（b）可以看出一般位置直线的投影特性如下：

（1）直线的三个投影仍为直线，但不反映实长；

（2）直线的各个投影均倾斜于投影轴，长度比实长短，且不能反映直线与投影面的真实倾角。

4.直线投影的定比性

直线上的点分割线段之比等于其投影之比，这称为直线投影的定比性。在图2-23（a）中，点C在线段AB上，它把线段AB分成AC和CB两段。根据直线投影的定比性可以得出AC∶CB＝ac∶cb＝a′c′∶c′b′＝a″c″∶c″b″[图2-23（b）］。

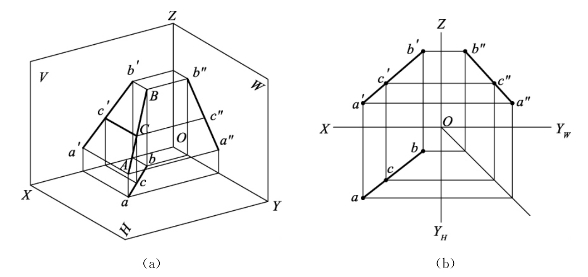
图2-23　直线投影的定比性

【例2】如图2-24（a）所示，已知直线AB，求作AB上的C点，使AC∶CB＝2∶3。

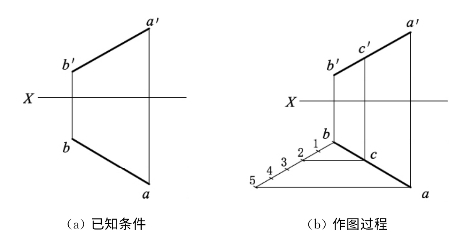
图2-24　求作直线上的点

【解】根据直线上的点的投影特性，作图过程如图2-24（b）所示：

（1）自a任引一直线，以任意直线长度为单位长度，从a顺次量相等的5个单位，得点1，2，3，4，5。

（2）连5与b，作2c∥5a，与ab交于c。

（3）由c引投影连线，与a′b′交得c′，c′与c即为所求的C点的两面投影。

5.两条直线的相对位置

两条直线在空间的相对位置关系有平行、相交和交叉（异面）三种情况。

（1）两直线平行(www.daowen.com)

若空间两直线平行，则它们的各同面投影必定互相平行。如图2-25所示，由于AB∥CD，则必定ab∥cd，a′b′∥c′d′，a″b″∥c″d″。反之，若两直线的各同面投影互相平行，则此两直线在空间也必定互相平行。

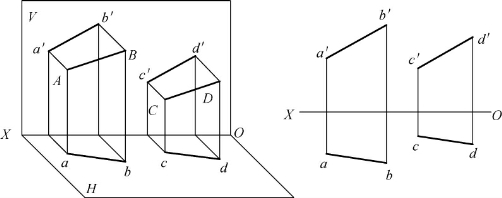
图2-25　两直线平行

（2）两直线相交

若空间两直线相交，则它们的各同面投影必定相交，且交点符合点的投影规律。如图2-26所示，两直线AB、CD相交于K点，因为K点是两直线的共有点，则两直线的各组同面投影的交点k、k′、k″必定是空间交点K的投影。若两直线的各同面投影相交，且各组同面投影的交点符合点的投影规律，则此两直线在空间也必定相交。

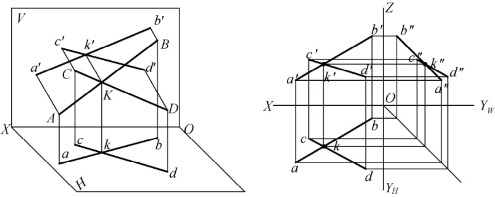
图2-26　两直线相交

（3）两直线交叉

既不平行也不相交的两直线，称为交叉（异面）直线。其各面投影既不符合平行两直线的投影特性，也不符合相交两直线的投影特性，如图2-27所示。

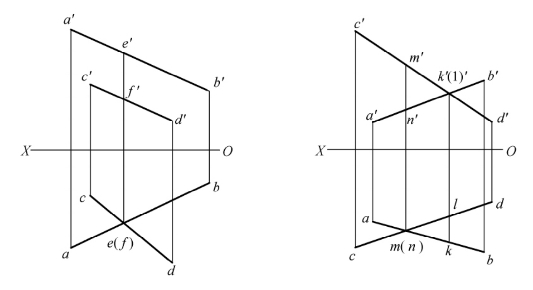
图2-27　两直线交叉

【例3】如图2-28（a）所示，试判断K点是否在侧平线MN上？

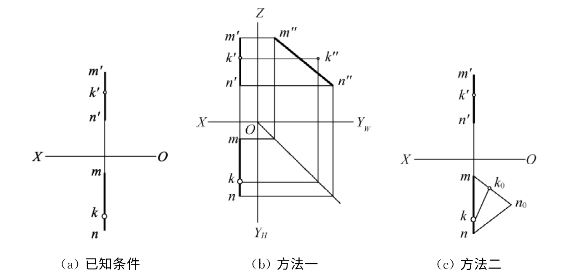
图2-28　例3图示

【解】可按直线上点的投影特性，用方法一或方法二进行判断。

方法一，如图2-28（b）所示：

（1）加W面，即过O作投影轴OYH、OYW、OZ。

（2）由m′n′、mn和k′、k作出m″n″和k″。

（3）由于k″不在m″n″上，所以K点不在MN上。

方法二，如图2-28（c）所示：

（1）过m任作一直线，在其上取mk0＝m′k′，k0n0＝k′n′。

（2）分别将k和k0、n和n0连成直线。

（3）由于kk0∥\nn0，于是m′k′∶k′n′≠mk∶kn，从而就可立即判断出K点不在MN上。

（三）平面的投影规律

平面与投影面的相对位置有三种：投影面垂直面、投影面平行面和一般位置平面。平面对H、V、W面的倾角分别用α、β、γ来表示。

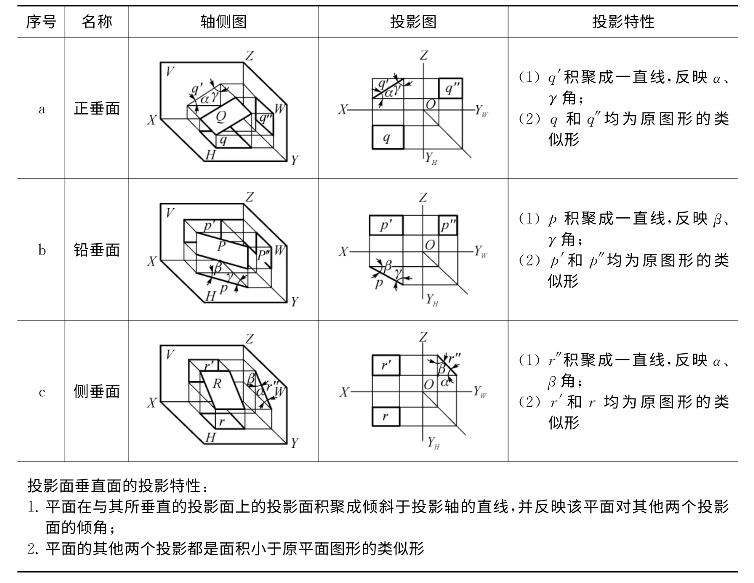
1.投影面垂直面

垂直于一个投影面，与另两个投影面倾斜的平面称为该投影面的垂直面。垂直于V面的平面称为正垂面；垂直于H面的平面称为铅垂面；垂直于W面的平面称为侧垂面（表2-3）。

表2-3　投影面垂直面的投影特性

2.投影面平行面

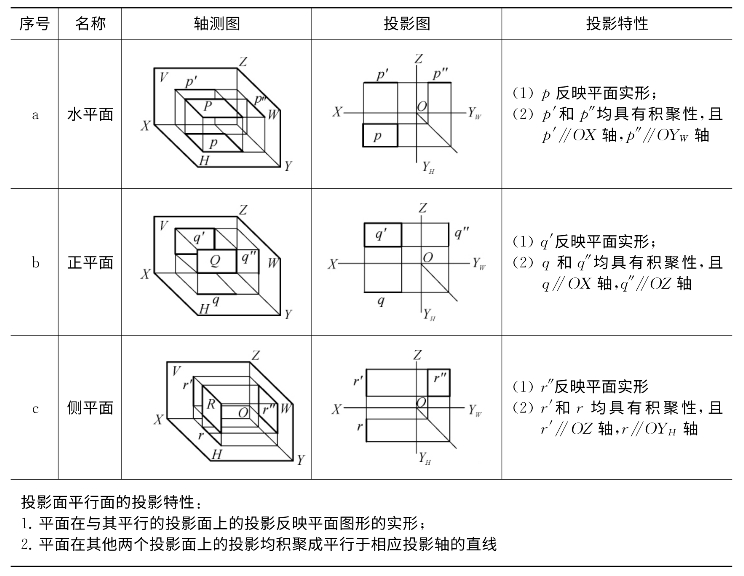
平行于一个投影面，与另两个投影面垂直的平面称为该投影面的平行面。平行于V面的平面称为正平面；平行于H面的平面称为水平面；平行于W面的平面称为侧平面（表2-4）。

表2-4　投影面平行面的投影特性

3.一般位置平面

倾斜于三个投影面的平面，称为一般位置平面，其投影如图2-29所示（图中平面用三角形表示）。△ABC对H、V、W面均倾斜，它的三个投影都是三角形，为原平面图形的类似形，面积均比实形小。

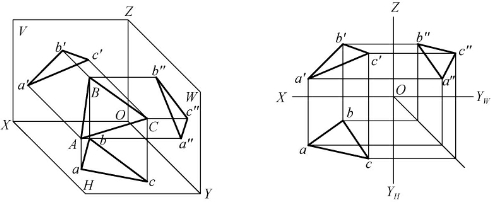
图2-29　一般位置平面

特殊位置上的点、直线和图形，在该平面的有积聚性的投影所在的投影面上的投影，必定积聚在该平面的有积聚性的投影上。利用这个投影特性，可以求做特殊位置平面上的点、直线和图形的投影。

【例4】如图2-30（a）所示，已知△ABC，在△ABC上求作一条距V面为13mm的正平线。

【解】作图过程如图2-30（b）所示：

（1）在OX轴之下（即OX轴之前）13mm处，作OX轴的平行线，即为这条正平线的H面投影，与ab、bc分别交得d、e，de即为所求作的正平线DE的H面投影。

（2）由d、e作投影连线，分别与a′b′、b′c′交得d′、e′，连接d′和e′，d′e′即为所求的正平线DE的V面投影。

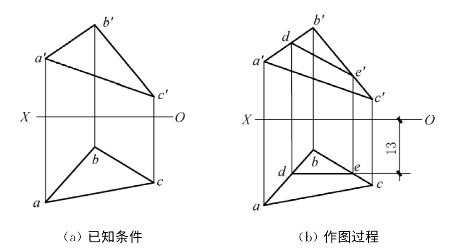
图2-30　在△ABC上求作正平线