工程中最常用的投影法是平行投影法中的正投影法。了解正投影的基本性质，对分析和绘制物体的正投影图至关重要。点、直线、平面是形成物体的最基本几何元素，在学习投影方法时，应该首先了解点、直线和平面的正投影的特性。点、直线和平面在正投影中具有以下基本特性。

1.同素性（类似性）

一般情况下，点的正投影仍然是点，直线的正投影仍为直线，平面的正投影仍为原空间几何形状的平面，这种性质称为正投影的同素性（类似性）。

如图2-6（a）所示，自点A向投影面H（H表示该投影面为水平面）引一条铅垂线（投影线），所得垂足a即为点A在H面上的正投影，点的投影仍是点；在图2-6（b）中，过直线BC向投影面H作垂面，所得交线bc即为直线BC在H面上的正投影，bc仍然为直线，但bc的长度小于直线的原长；在图2-6（c）中，过平面KLMN向投影面H作垂线，所得交面klmn为平面KLMN的正投影，klmn仍为四边形平面，但klmn图形的面积小于空间平面的面积。

图2-6　正投影的同素性（类似性）

2.从属性

点在直线上，点的正投影一定在该直线的正投影上。点、直线在平面上，点和直线的正投影一定在该平面的正投影上，这种性质称为正投影的从属性。

如图2-7（a）所示，点K在直线BC上，点K的投影k在直线BC的投影bc上；如图2-7（b）所示，点D和直线EF在KLMN平面上，点D和直线EF的投影d和eƒ在平面的投影klmn上。

图2-7　正投影的从属性

3.定比性

线段上的点将该线段分成的比例，等于点的正投影分线段的正投影所成的比例，这种性质称为正投影的定比性。如图2-7（a）所示，点K将线段BC划分的比例，等于点K的投影k将线段BC的投影bc划分的比例，即BK∶KC＝bk∶kc。

4.平行性(www.daowen.com)

图2-8　正投影的平行性

两直线平行，则其正投影也平行，且空间线段的长度之比等于它们正投影的长度之比，这种性质称为正投影的平行性。如图2-8所示，空间直线AB∥CD，则直线AB、CD的正投影ab、cd也相互平行，即ab∥cd，且AB∶CD＝ab∶cd。

5.全等性（显实性）

当线段或平面平行于投影面时，其线段的投影长度反映线段的实长；平面的投影与原平面图形全等。这种性质称为正投影的全等性。如图2-9所示，线段AB平行于H面，则AB的正投影ab＝AB；平面EFGH平行于H面，则平面EFGH的正投影eƒgh≌EFGH。

6.积聚性

当直线或平面垂直于投影面时，其直线的正投影积聚为一个点；平面的正投影积聚为一条直线。这种性质称为正投影的积聚性。如图2-10所示，直线AB垂直于H面，则AB的正投影a（b）积聚为一点；平面EFGH垂直于H面，则平面EFGH的正投影e（h）ƒ（g）积聚为一条直线。

图2-9　正投影的全等性（显实性）

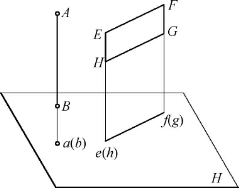
图2-10　正投影的积聚性

图2-11　物体的单面投影

上述正投影的基本性质中，要特别注意正投影中的不变性（如同素性、点和直线的从属性、两直线的平行性等）和定比性，这对解决空间问题有着至关重要的作用。