1）个体层面因素对教师参与产学合作广度的影响分析

以教师参与产学合作的广度为因变量，教师个体层面因素为自变量，建立回归模型，探讨教师个体层面因素对教师参与产学合作广度的影响。

（1）多元回归分析的三大检验。为了保证正确使用多元线性回归模型以便得出科学的结论，必须检验回归模型是否存在多重共线性、序列相关和异方差等三大问题（马庆国2002）。

①多重共线性检验。多重共线性问题的检验可以通过容差和膨胀因子（VIF）来检验。依照吴明隆（2010）的观点，容差的值介于0到1之间，如果其值越接近于0，表明共线性越严重，一般判断是，容差的值小于0.1，就可能存在共线性问题。另外，VIF越小，表明自变量间的共线性越不明显，一般判断是，如果VIF大于10，就表明自变量可能存在多重共线性问题。

②序列相关问题检验。一般通过DW值来检验模型中是否存在序列相关问题（吴明隆2010），DW的值在0—4之间，越接近于2，表明存在序列相关的可能性越小。因为本研究的数据是截面数据，所以不太可能出现序列相关问题。从表5-21也可以看出，DW值非常接近于2，说明回归模型不存在序列相关问题。

表5-21　个人层面因素对教师参与产学合作广度影响的多元回归模型汇总表

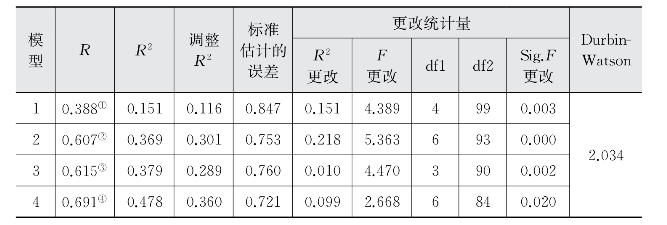
①预测变量：（常量），学术职称（教授为1），学科（工科为1），性别（男性为1），年龄。
②预测变量：（常量），学术职称（教授为1），学科（工科为1），性别（男性为1），年龄，动机——兴趣，动机——荣誉，动机——社会责任，动机——资金，动机——研究，动机——学生。
③预测变量：（常量），学术职称（教授为1），学科（工科为1），性别（男性为1），年龄，动机——兴趣，动机——荣誉，动机——社会责任，动机——资金，动机——研究，动机——学生，学生时代训练，社会资本，产学合作经验。
④预测变量：（常量），学术职称（教授为1），学科（工科为1），性别（男性为1），年龄，动机——兴趣，动机——荣誉，动机——社会责任，动机——资金，动机——研究，动机——学生，学生时代训练，社会资本，产学合作经验，政府资金占比，SCI数量，总研究资金，专利数量，产学合作时间占比，产业资金占比。
⑤因变量：教师参与四类产学合作的广度。

③异方差问题检验。样本观察值要符合正态性和方差齐性假定，这个假定可以通过标准化残差散点图来检验。若散点图的点在0值上下呈水平随机分布时，表示样本观察值符合正态性和方差齐性假定（吴明隆2010）。从图5-8可以看出，本回归模型不存在异方差问题。

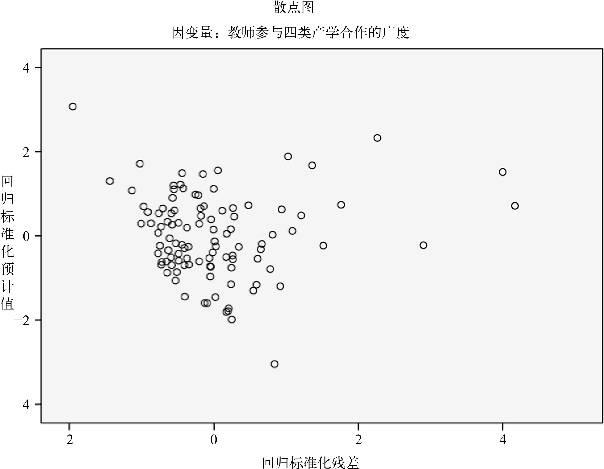
图5-8　个人层面因素对教师参与产学合作广度影响的回归模型残差散点图

（2）回归结果分析。本研究采用逐步进入的方式来构建回归模型，具体回归结果（见表5-21～表5-23）。

表5-22　个人层面因素对教师参与产学合作广度影响的多元回归模型方差统计表

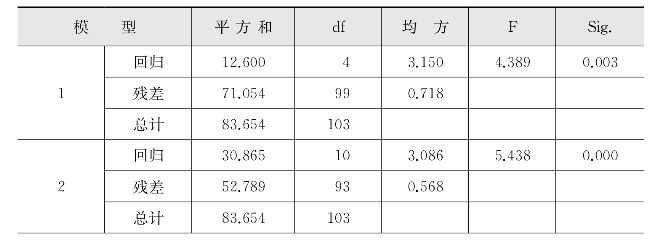
（续表）

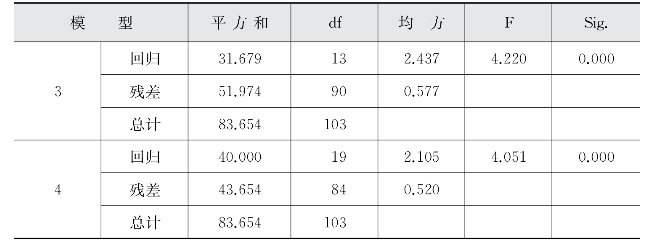
表5-23　个人层面因素对教师参与产学合作广度影响的回归分析结果

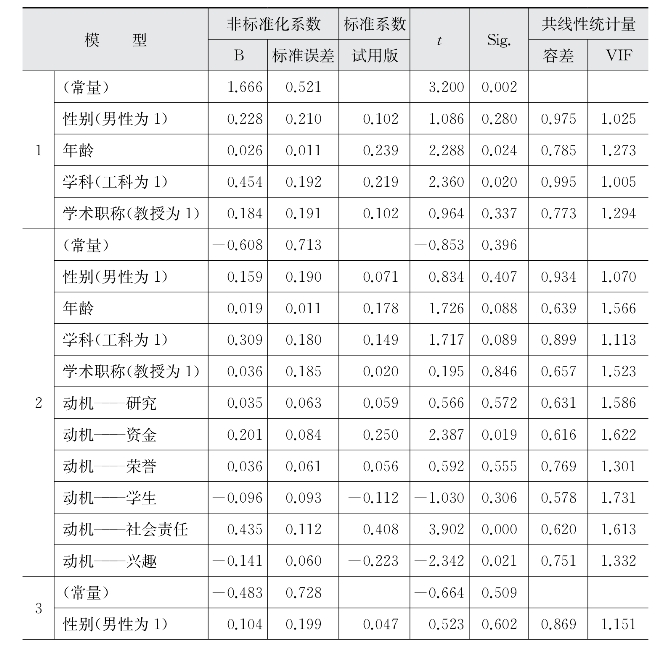
（续表）

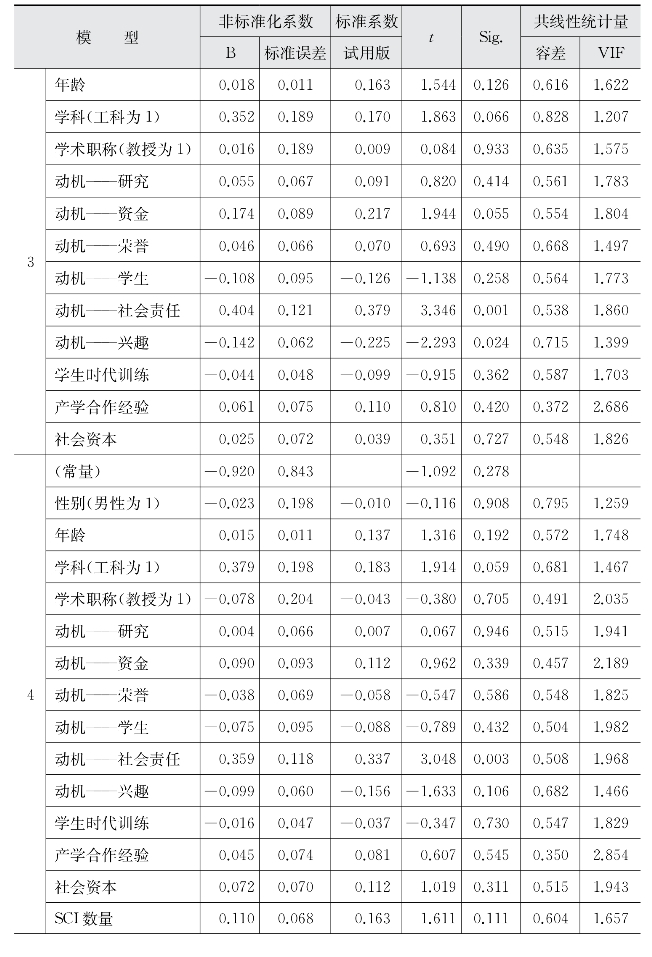
（续表）

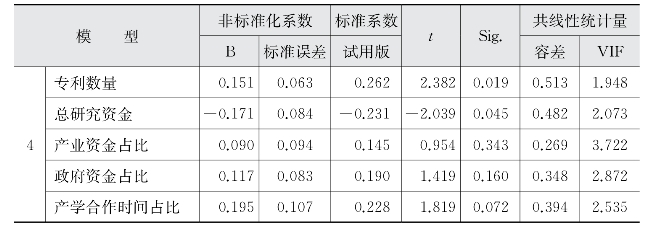
①因变量：教师参与四类产学合作的广度(www.daowen.com)

第一组进入的自变量是性别、年龄、学科、学术职称（模型1）。模型1的R2为15.1%，说明这4个变量组成的多元回归方程解释了教师参与产学合作广度总体变差的15.1%。模型1的F统计量为4.389，相应的p值为0.003，小于0.01的显著性水平，表示因变量与自变量之间的线性关系是显著的。在回归系数的显著性检验中，年龄和学科均在0.05的显著性水平上显著，说明年龄和学科对教师参与产学合作的广度有显著影响，而且从系数来看，均呈显著正向影响。性别和学术职称的回归系数则没有达到显著性水平，说明性别和学术职称对教师参与产学合作的广度没有显著影响。

第二组进入的自变量是动机，分别为研究、资金、荣誉、学生、社会责任和兴趣（模型2）。加入第二组变量后，R2为36.9%，说明加入第一组变量和第二组变量组成的多元回归方程共同解释了教师参与产学合作广度总体变差的36.9%，而且R2的显著增加说明第二组的加入使得回归方程的拟合度越来越好。模型2的线性关系同样显著（p=0.000）。在回归系数的显著性检验中，资金动机、社会责任动机、兴趣动机分别在0.05、0.01、0.05的显著性水平上显著，其中资金动机和社会责任动机对教师参与产学合作的广度有显著正向影响，而兴趣动机的回归系数为负数，说明其对教师参与产学合作的广度有显著负向影响。

第三组进入的自变量是人力资本，分别为学生时代的训练、产学合作经验、社会资本（模型3）。模型3的R2为37.9%，比模型2只增加了1%，说明第三组自变量的加入对回归模型拟合优度的增加贡献不大。模型3的线性关系同样显著（p=0.000）。在回归系数的显著性检验中，没有自变量在规定的显著性水平上显著，说明第三组变量中没有变量对教师参与产学合作的广度有显著影响，这也印证了第三组变量对R2贡献不大。

第四组进入的自变量是学术研究，分别为SCI数量、专利数量、总研究资金、产业资金占比、政府资金占比、产学合作时间占比（模型4）。加入最后一组变量后，R2为47.8%，比模型3增加了10%左右，说明第四组变量的增加使得回归模型的拟合度越来越好。模型4的线性关系同样显著（p=0.000）。在回归系数的显著性检验中，专利数量、总研究资金、产学合作时间占比分别在0.05、0.05、0.1的显著性水平上显著，但是总研究资金对教师参与产学合作的广度有显著负向影响。虽然SCI数量的回归系数显著性为0.111，超过了0.1的显著性水平，但是接近0.1，故仍然考虑将其认为对教师参与产学合作的广度有显著正向影响。其他变量则对因变量没有显著的正向或负向影响。

经过对上述四个多元回归模型的分析，得到了个人层面对教师参与产学合作广度有显著影响的因素：年龄、学科、资金动机、社会责任动机、兴趣动机、SCI数量、专利数量、总研究资金、产学合作占比，其中兴趣动机和总研究资金对教师参与产学合作的广度呈显著的负影响，其他均呈现显著的正向影响，而剩下的其他因素对教师参与产学合作的广度没有显著影响，对结果的具体解释分析将在得出所有回归模型后一并展开。

2）三个层面因素对教师参与产学合作广度的回归分析结果汇总

按照上述回归分析的方法和步骤，构建了院系层面因素对教师参与产学合作的广度的回归模型（见模型1-5～模型1-7），以及学校层面因素对教师参与产学合作的广度的回归模型（见模型1-8～模型1-10）。

模型1-5进入的变量是学科和跨组织工作；模型1-6增加的变量是院系环境因素变量；模型1-7增加的变量是院系研究能力变量。

模型1-8进入的变量是大学分类；模型1-9增加的变量是大学产学合作氛围变量；模型1-10增加的变量是大学研究能力和研究经费变量。

经过多个回归模型的构建和分析，得出了表5-24的结果，汇总了个人层面、院系层面和学校层面对教师参与产学合作广度的回归结果（表中数据为回归系数及其显著性）。

表5-24　教师参与产学合作广度影响的回归模型结果汇总

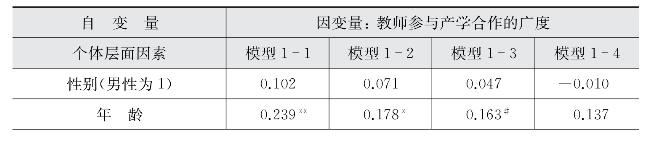
（续表）

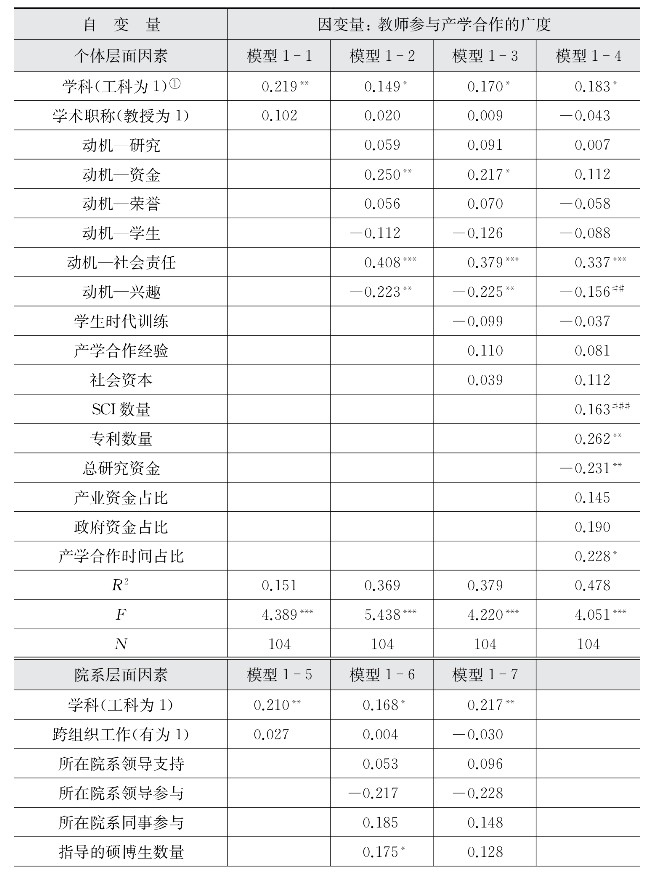
①　虽然在个人层面因素中加入了学科因素，但是按照理论框架，在院系层面讨论学科因素，所以个人层面对学科因素不进行讨论。

（续表）

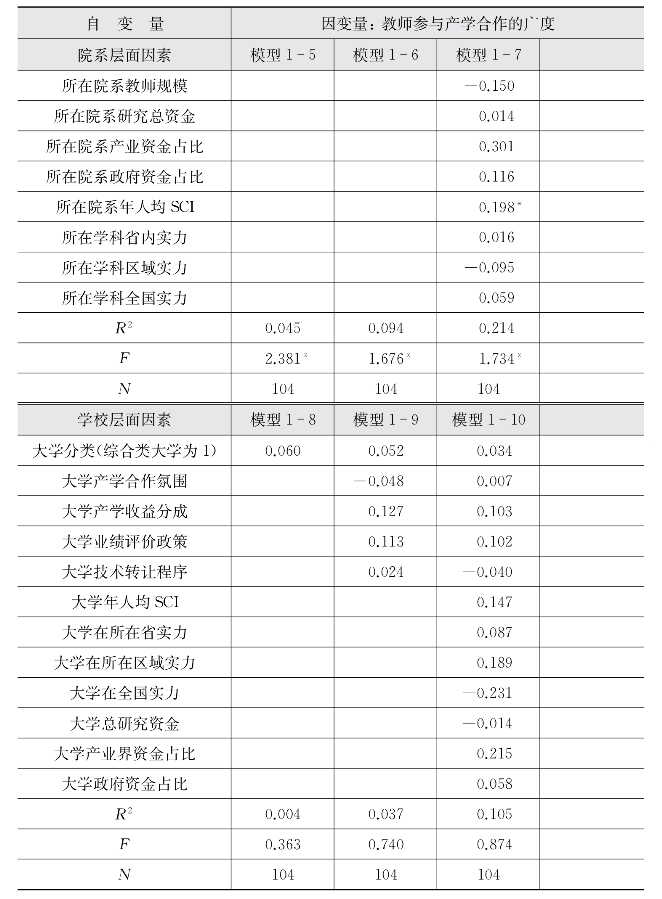
*p＜0.10，**p＜0.05，***p＜0.01
#p=0.126，##p=0.106，###p=0.111

3）线性回归结果分析

模型1-1～模型1-10分别探讨了个人层面因素、院系层面因素、学校层面因素对教师参与产学合作方式广度的影响。从表5-24可见，学校层面因素对教师参与产学合作的广度的三个回归方程的F统计量均不显著，说明学校层面的自变量与因变量线性关系不显著，从回归系数显著性也可以发现，学校层面的因素对教师参与产学合作广度均不产生显著影响。

从个人层面因素来看，显著影响教师参与产学合作广度的因素有：年龄、资金动机、社会责任动机、兴趣动机、SCI数量、专利数量、总研究资金、产学合作时间占比等几个因素，其中兴趣动机、总研究资金对教师参与产学合作广度呈显著负向影响。

从院系层面来看，对教师参与产学合作广度有显著影响的因素有学科、指导的硕博生数量、所在院系年人均SCI数量等。