1.用辅助平面法求相贯点的原理

辅助平面法就是用辅助平面同时截切两相贯体，找出截面与交线的交点——相贯点。如果把一个相贯体特别是在任何投影面上都不能反映实形的相贯线，用若干辅助平面同时截切相贯部分，就可以得到若干个相贯点，如图2⁃33所示，那么相贯线也就可以很容易地连接起来。

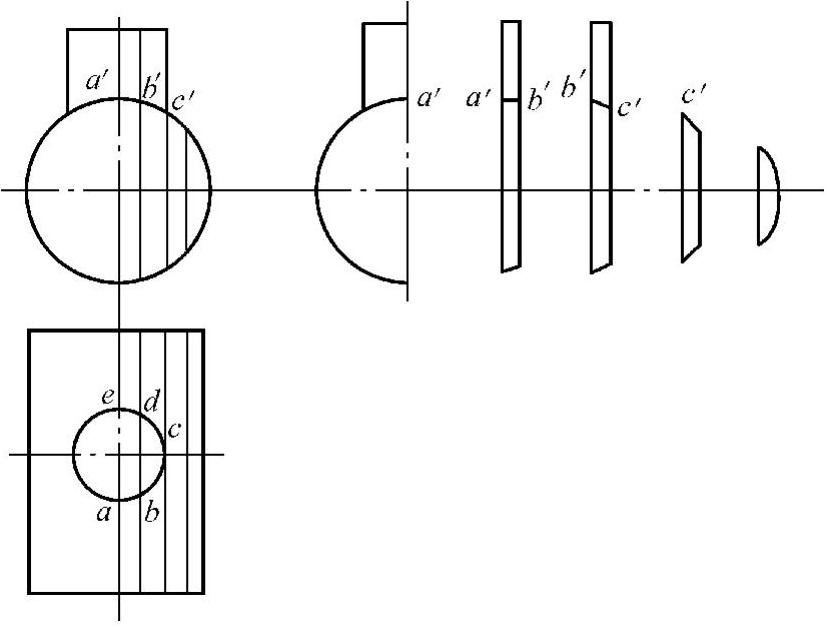
图2⁃33 辅助平面法求相贯线原理图

为了使作图简便，选择辅助平面应根据以下原则：

1）辅助平面必须同时过两形体和两形体的相贯处。

2）截交线应是最简单的几何图形。

3）截交平面一般应平行于正投影、垂直于水平投影，这样才方便分别展开投影。

2.用辅助平面法求作两圆柱相贯的相贯线(www.daowen.com)

如图2⁃34所示，由于圆柱前后左右对称相交，在俯视图上，小圆柱积聚为一个圆。在左视图上，大圆柱积聚为一个圆，b′、d′两点是主视图相贯最远的两点，且是左视图相贯的最高点。用辅助平面法求相贯点具体作图步骤如下：

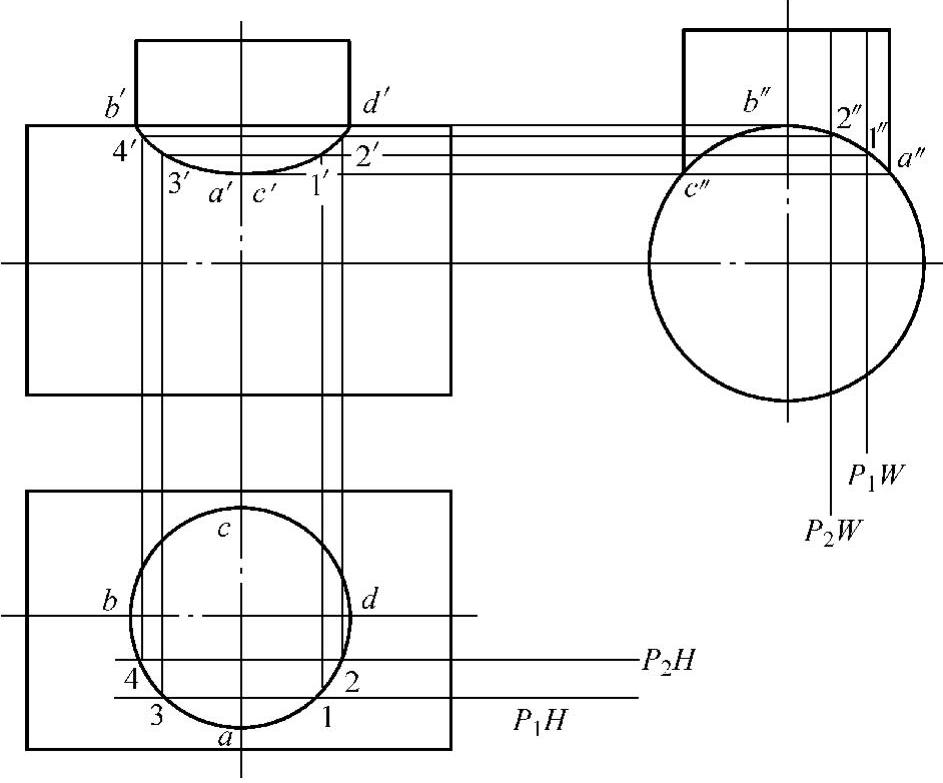
图2⁃34 用辅助平面法求作两圆柱相贯的相贯线

1）确定辅助平面P₁、P₂，使之平行于正投影面，在俯视图中与小圆相交于点1、2，在左视图中交于大圆上的1″、2″两点。

2）按照辅助平面法原理过俯视图1、2各点向上引垂线与左视图过点1″、2″引的水平线交于1′、2′点。4′、3′作法同理。

3）光滑连接b′、4′、3′、a′（c′）、1′、2′、d′各点即得圆柱的相贯线。

4）从相贯线处分解两圆柱体，用平行线法分别展开。