一个形体如果被几个水平面截切，所得到的一系列水平截交线就叫作纬线，对于旋转体如果轴线垂直于水平面，则纬线一定为一个圆，即为纬圆。

1.用纬线法求相贯线的原理

用纬线法求相贯线的原理是：若过形体表面任一点作水平切面的截切形体，可得到一条纬线，那么该点必定在该纬线上，只要把该纬线投影到另一视图上，就可求出该点在另一视图上的投影。如在相贯体上作适当数量的纬圆，便可得许多的相贯点，将相贯点平滑相连即可得两形体的相贯线。

已知点A，求A点在俯视图上的投影，如图2⁃31所示：

1）过锥面上任一点A作水平的截切形体，交锥面于b′c′两点。

2）过b′点引垂线交俯视水平中心线于b点。

3）以o为圆心，以ob为半径在俯视图上作纬圆。

4）过a′点作垂线交纬圆于a点，则a点为A点在俯视图上的投影。

5）按素线法即可再在左视图的截切圆上作出A点在左视图上的投影a″点。

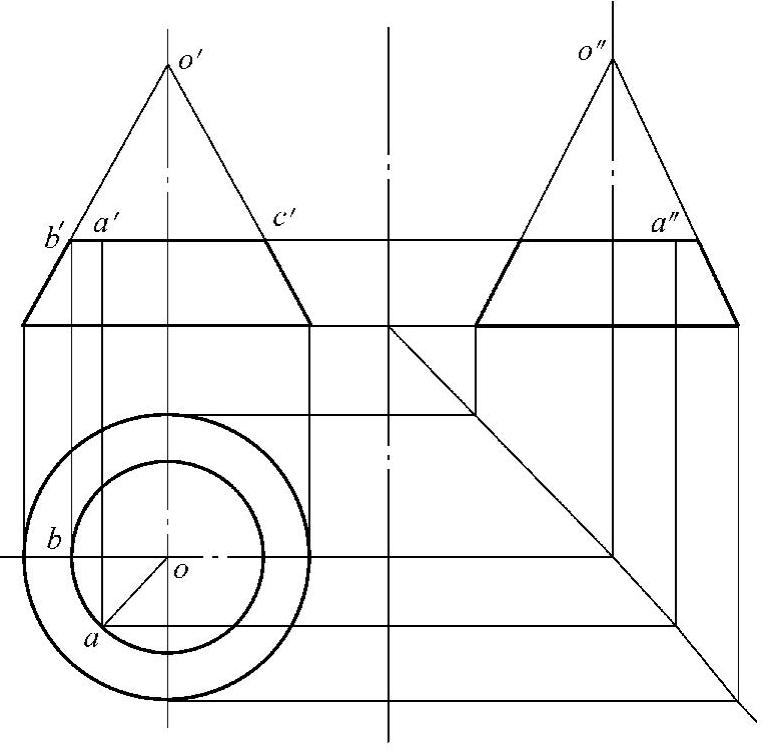
图2⁃31 用纬线法求A点在俯视图上的投影

2.用纬线法求圆柱面侧面直交正圆锥面的相贯线及其展开图(www.daowen.com)

如图2⁃32所示，该两曲面相交相贯线为一封闭空间曲线。圆柱面轴线垂直水平面，相贯线在俯视图中积聚成圆，过相贯体相交部分作适当截切纬圆，即可求出主视图的相贯线。

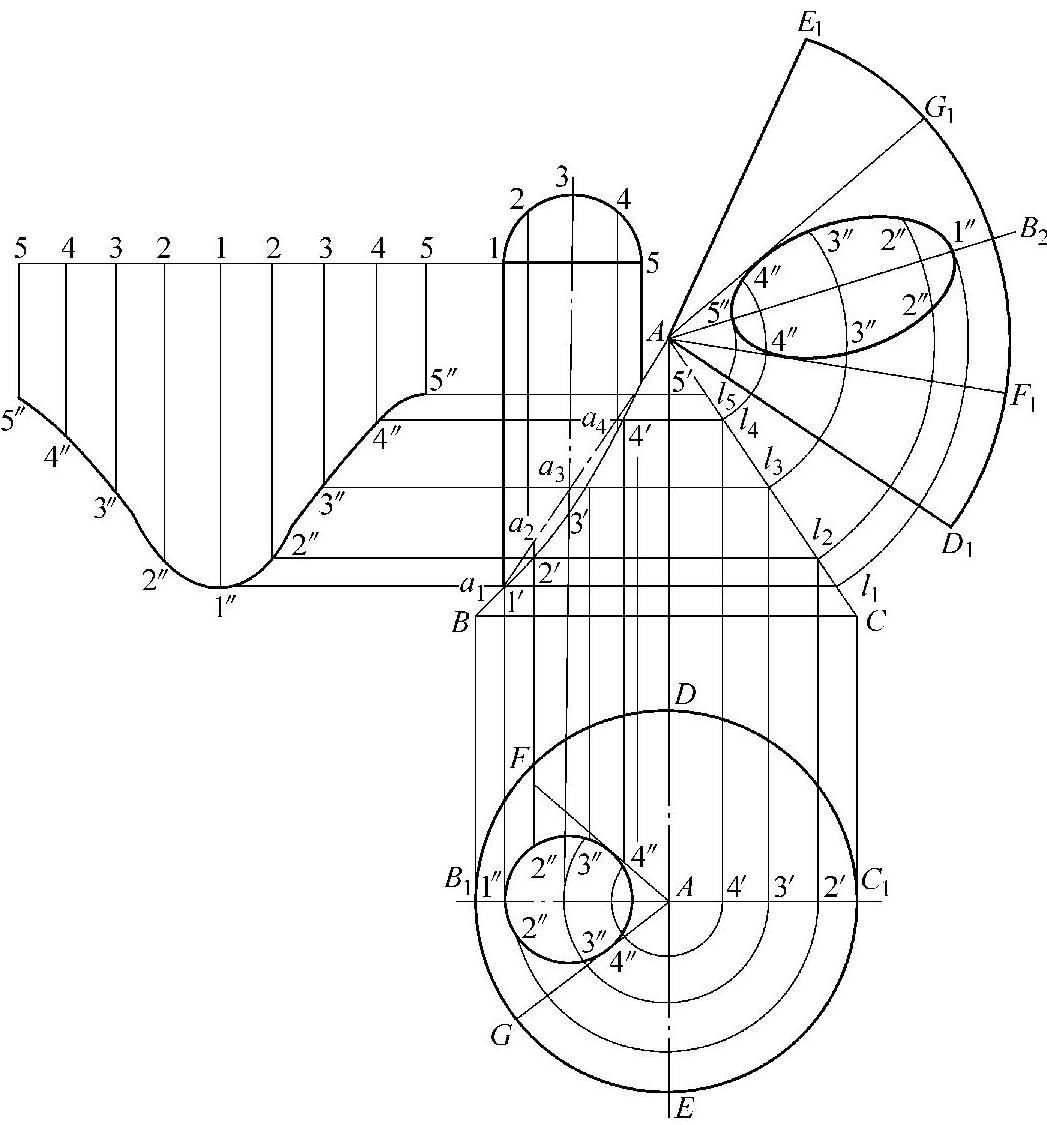
图2⁃32 用纬线法求圆柱面侧面直交正圆锥面的相贯线及其展开图

1）由已知尺寸画出形体放样图。圆柱面与圆锥面相交最高点5′，最低点1′。将圆柱面半圆4等分并引垂线交圆锥面轮廓线于2′、3′、4′三点；过3′、4′、5′点作圆锥体纬线截切线，交锥面另一边于1″、2″、3″、4″、5″各点，并过这五点作垂线与俯视图水平中心线相交。

2）分别以各截切纬线的实长为半径，以俯视图为圆心作纬圆，交圆柱面投影于2″、3″、4″各点；过2′、3′、4′向主视图引垂线，对应交2′2′、3′3′、4′4′。纬线于2′、3′、4′各点；光滑连接1′、2′、3′、4′、5′各点，即得到该形体在主视图上的相贯线。

3）用平行线法画出斜截圆柱面展开图。

4）用放射线法画出正圆锥展开图。

5）在圆锥面展开图上画出相贯线展开图：

①分别以a为圆心以O′1′、O′2″、O′3″、O′4″、O′5″为半径画弧，交锥面展开图中线于a、b、o、d、e点。

②以锥面中心线为轴线，分别过b、c、d各点，对应截取圆柱四纬圆交点得6个端点。

③分别光滑连接a与e间6点，即得到锥面展开图的相贯线。