素线法是利用素线作为辅助线与两形体相交以求相贯线的作图方法。

1.用素线法求相贯点的原理

用素线法求相贯点的原理：设想圆锥面是由许多素线所组成的，圆锥面上任一点必然在过该点的素线上，只要求出该点的素线投影，即可求出该点的投影。

如前所述，左视图上的投影求相贯线的关键是求相贯点，如图2⁃29所示。

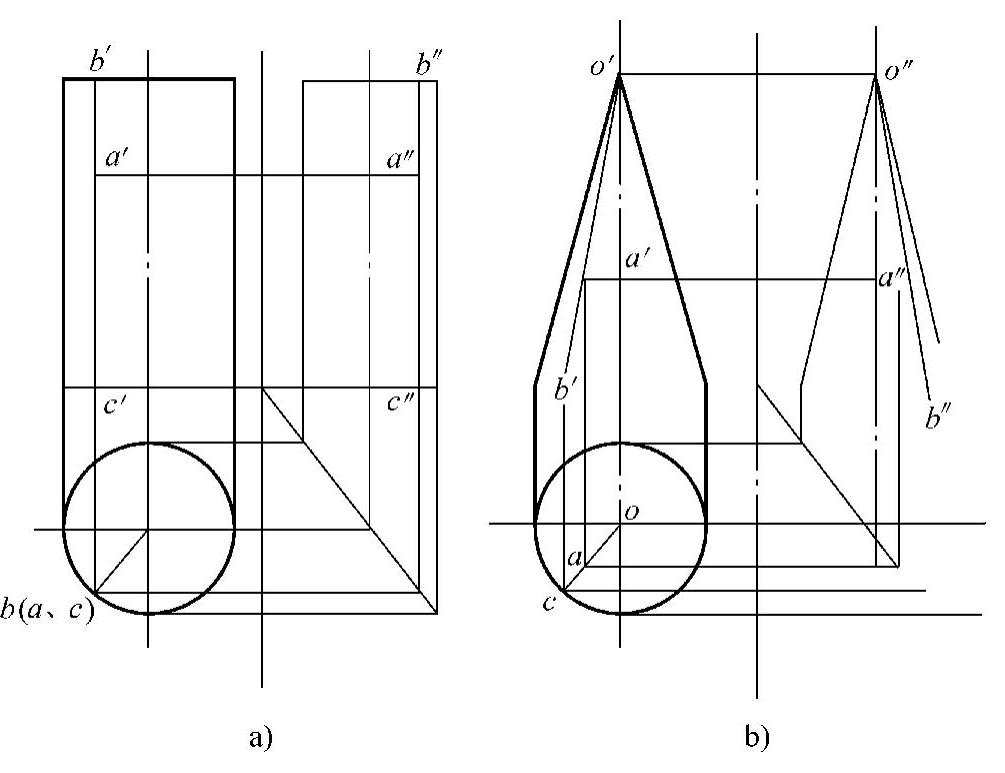
图2⁃29 用素线法求圆柱、圆锥表面点投影

用素线法作已知相贯点的投影可归纳如下：

1）在有已知点视图上作过已知点的素线。

2）将该素线投影到另一视图上。

3）最后将已知点投影到另一视图的相应素线上。(www.daowen.com)

2.用素线法求相贯线的实例

如图2⁃30所示，该形体在左视图上的相贯线为已知，只要按此视图确定素线位置，就可求出另外两图的相贯线，并绘制出两形体的展开图。

其作图步骤如下：

1）由已知尺寸，画出主视图与左视图的轮廓线。将左视图上H1′、G1′延长交于O点，使其成一正圆锥；并以圆锥底长为直径在锥底对应位置画出锥底面半圆周；6等分半圆周；过等分点1、2、3、4、3、2、1引垂线与底边交于点2″、3″、4″、3″、1″；连接O₁1″、O₁2″、O₁3″、O₁4″、O₁3″、O₁2″、O₁1″交已知左图相贯线于点1′、2′、3′、4′、3′、2′、1′。

2）主视图同样按左视图圆锥、锥底半圆的画法画出并6等分半圆，画出相应素线，只不过根据视图投影规律数字排列为4、3、2、1、2、3、4；过左视图相贯线各点水平线与主视图相对应各素线相交得4、3、2、1、2、3、4各点，平滑连接各点即得两形体相贯的主视图相贯线。

3）把两形体从相贯线处分解，用放射线法画出底边异形截头圆锥展开图。

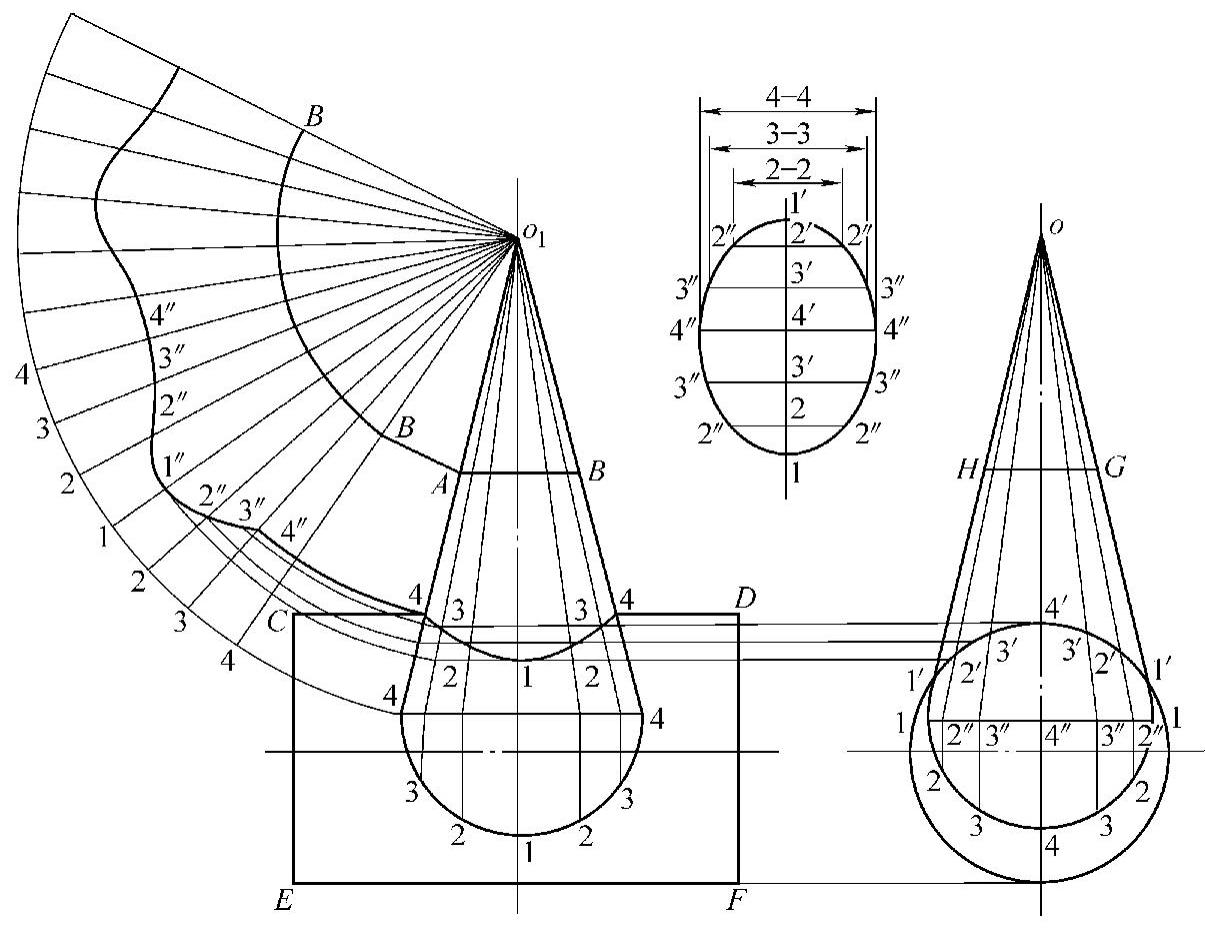
图2⁃30 用素线法求圆锥面直交圆柱面的放样图及展开图

4）用平行线法展开圆柱面及圆柱面上相贯部位的切孔。展开切孔时，作一直线1′1′＝1′1′弧长，即按左视图上各点间的对应弧，依次求得1′、2′、3′、4′、3′、2′、1′各点，过2′、3′、4′、3′、2′各点作直线与1′1垂直，并以1′1为轴线，在2′、3′、4′、3′、2′各点作出的轴线上按左视图相贯线，在2′－2′、3′－3′、4′－4′的距离上分别求得2″、2″、3″、3″、4″、4″各点，与轴线对称，用平滑曲线连接各点，即得到圆柱表面相贯线的展开图。