在钣金作业的放样与展开中，展开图就是钣金构件表面铺平后的实际形状尺寸图。为了求得各表面的实形，就必须求得构成表面各线段的实长。在各种形体中，有一部分处于特殊位置，即平行于投影面的线段可反映实长，但处于其他位置时却不能反映实长。这就必须通过作图法或计算法求得线段实长。常用的线段实长作图求法有直角三角形法、直角梯形法、旋转法和更换投影面法等，这里重点介绍常用的直角三角形法、直角梯形法和旋转法。

1.直角三角形法

直角三角形法就是作一个直角三角形，使这个直角三角形的一个直角边等于空间直线在某个视图中的边长，另一条直角边为该直线段在另一个视图中的空间距离（高度差），则斜边即为空间直线的实长。

如图2⁃8所示，已知空间线段BC的两面投影为bc和b′c′，求线段BC的实长。

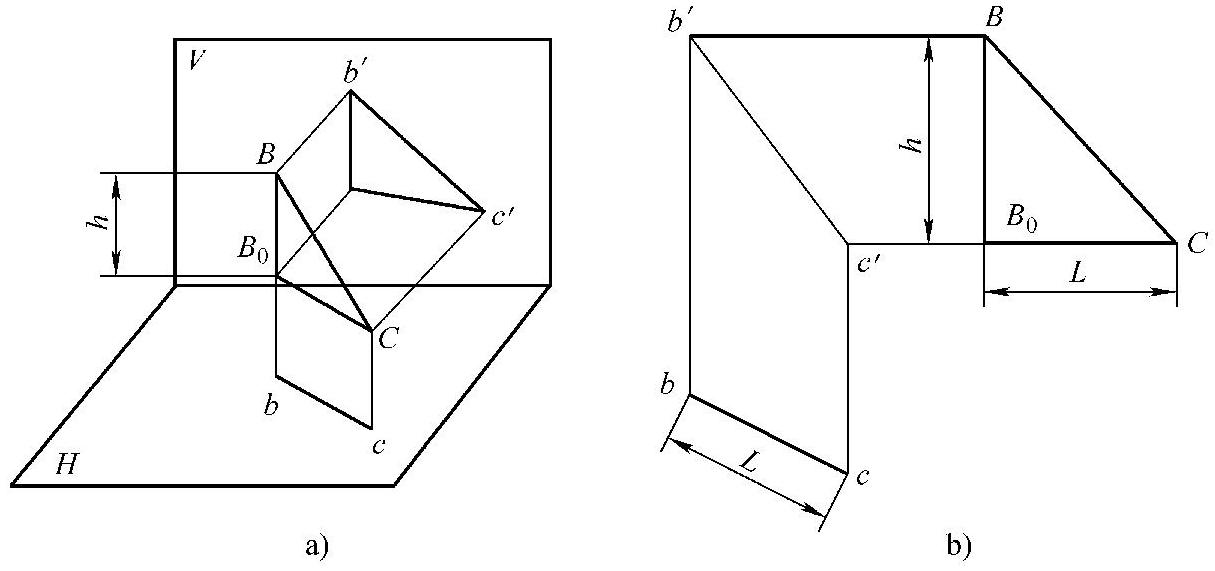
图2⁃8 用直角三角形法求线段实长

由于BC倾斜于两投影面，所以其投影bc和b′c′均不反映实长。这时作一辅助线B₀ C// bc，得直角△BB₀ C。

在直角△BB₀ C中，只要知道两个直角边BB₀和B₀ C，就可求出斜边BC。因为B₀ C等于bc，可以从水平投影中量得，又因为BB₀等于B点和B₀点的高度差h，可以从正投影中作图求得，因此，求BC实长的作图步骤如下：

1）作一直角三角形，令L＝bc为一直角边。

2）使bc的竖向距离（高度差）h为另一直角边。

3）斜边长即为线段BC的实长。

2.直角梯形法

直角梯形法就是以空间直线段在某个视图中的投影长为直角梯形的一个腰长，以空间直线段在另一个视图中的投影两端点到水平轴的垂直距离分别为直角梯形的两个底，则另一个腰长即为空间直线实长。

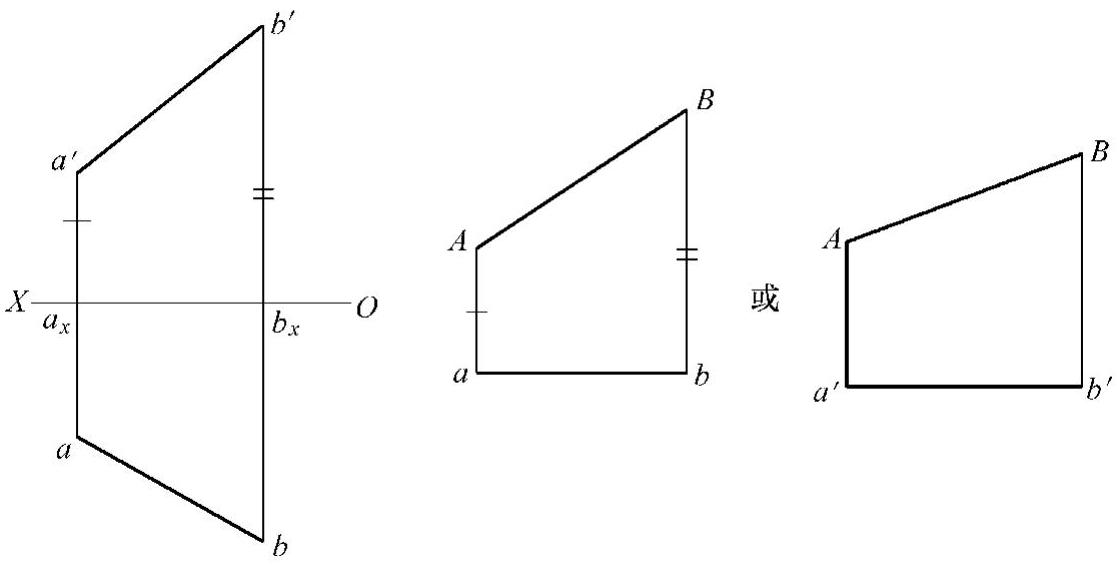
如图2⁃9所示，已知空间一般位置线段AB和两投影ab、a′b′，求空间线段AB实长。

(www.daowen.com)

图2⁃9 用直角梯形法求线段实长

作图步骤如下：

1）作一直线段，使其长等于ab。

2）过a、b分别作线段ab的垂线，使长度分别等于a′a和b′b。

3）连接梯形两端点，即为AB实长。

3.旋转法

旋转法就是保持投影面不变，使倾斜直线绕垂直于某一投影面的直线，旋转成与投影面相平行的直线，则直线在与其平行的投影面上的投影就反映它的实长。

如图2⁃10所示，已知空间直线段AB的两投影ab和a′b′，求AB实长。

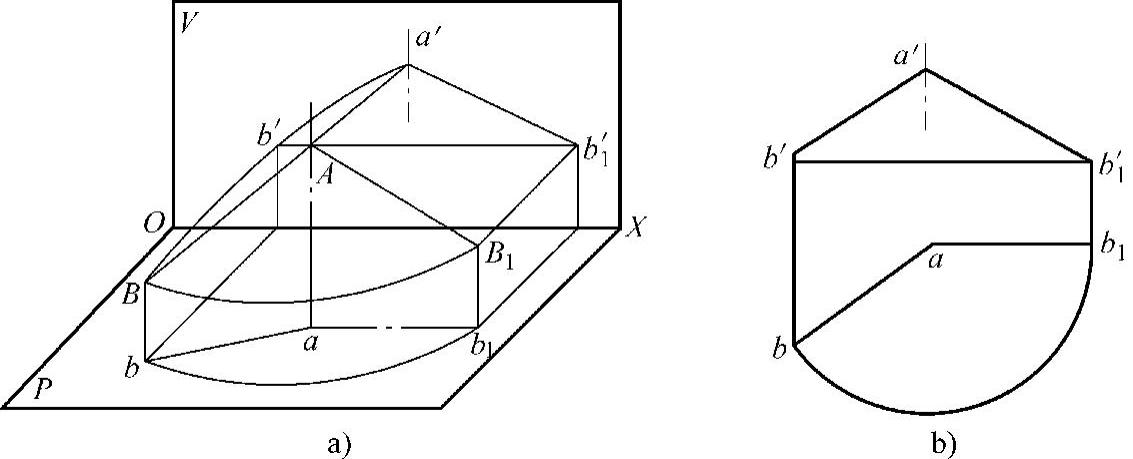
图2⁃10 用旋转法求线段实长

1）以a为圆心，把ab旋转到与投影面平行的位置ab₁。

2）过b′作与x轴平行的线，与过b₁所作的OX轴的垂直线交于b′₁点。

3）连接a′b′₁，即为AB实长。