【例6.1】使用程序SMIA对图6.6所示匀质梁（不计轴向变形，取EI=1、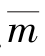=1、l=1）的自振频率进行分析。

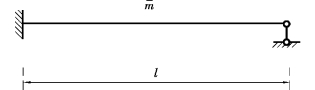
图6.6　自由振动分析

【分析】单元质量矩阵按集中质量模式形成时，不存在转动质量，动力自由度与体系分析总自由度不相等，矩阵经动力凝聚后，动力刚度方程阶数较少。

单元质量矩阵按一致质量模式形成时，集成的结构质量矩阵不存在0主元，动力自由度与体系分析总自由度相同。

【解】（1）取一个单元计算，如图6.7所示。

质量矩阵分别按集中质量模式和一致质量模式进行计算。集中质量模型中，未考虑转动质量的集成，而唯一影响结构刚度特征的自由度又为转动自由度，因此一个单元无法进行动力分析。

一致质量模型可顺利分析，计算可得频率ω=20.4939。计算结果与精确解相比，误差为+32.95%。

（2）取两个单元进行计算，如图6.8所示。集中质量模式下为单自由体系（无转动自由度）；而一致质量模式下，动力自由度为3，仍等于结构分析的总自由度。

图6.7

图6.8

两种方式下所得各阶频率，及与解析解间误差如下所示：(www.daowen.com)

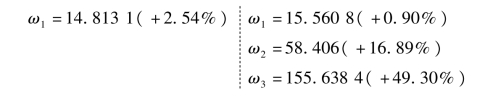
（3）取5个单元进行计算。如图6.9所示。此时集中质量模式动力自由度数目为4（无转动自由度），而一致质量模式下动力自由度数目则为9。

图6.9

两种方式下所得各阶频率，及与解析解间误差如下所示：

【说明】

（1）一致质量矩阵在一定程度上考虑了单元质量分布的影响，相同单元数下，同阶频率的计算精度，相较于集中质量模式有明显改善。

（2）一致质量矩阵模式下，可以考虑转动自由度，动力自由度数目更多。但根据最后的精度比对，一致质量模式对转动质量的描述并不太好，所对应高阶频率精度都较差。

（3）两种方式都可以使用增加单元数目的方法，提高低阶频率的计算精度。

对于等截面匀质杆元，一致质量矩阵尽管有更多动力自由度和更良好的精度，但单元数选定后，高阶振型误差仍无法让人满意。

其原因主要在于，根据等截面匀质杆的解析计算，精确的振型曲线应是双曲函数与三角函数的线性叠加，即如式（a）所示：

而一致质量矩中使用的位移插值函数，是三次多项式，显然无法精确描述单元真实振型曲线下的变形。