1）自振频率

ωi为结构自振频率。工程分析时常将自振频率从小到大进行排列。

自振频率为标量，与坐标系统选择无关，在主坐标空间和任意广义坐标空间下都一致。

在可解耦的广义坐标空间下，各自由度的运动是非耦合的，便于独立进行讨论。对应此广义坐标空间，有：

由上式可知：可解耦的广义坐标系统下，广义质量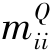越大，广义刚度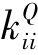越小，则对应阶的自振频率越小。而质量大，则惯性力越大；刚度小，则运动响应也更大。因此，若广义荷载的各阶量级相近，则对应于低阶频率，结构的动力响应一般也会更大一些。而随着进入高阶，即意味着广义质量开始减小，而广义刚度有所增加，同时据相关研究结果，高阶响应时，阻尼会明显增强，则动力响应自然会相应减小。

故在结构动力分析时，可只考虑低阶响应，而对于高阶分量的贡献则截断不作分析（从小到大排列自振频率的原因即在于此），对结构计算误差影响不大。

但应注意，这是以自由振动的分析结果作出的定性判断。当激励荷载直接作用于结构时，如果动力荷载恰好对应于高阶广义自由度，仍在低阶作截断或会引起较大误差。

2）主振型

特征向量Ti，也称为主振型，对应于各阶自振频率ωi。

各阶振型按列方式进行排列，得到的矩阵即坐标变换矩阵T，也称为主振型矩阵。从前面的分析可知，主振型矩阵实质上为一坐标变换矩阵。根据求解过程（式6.21）可知，某阶振动形式以列向量Ti或cTi表达。(www.daowen.com)

为便于特征分析，可根据质量矩阵对主振型矩阵进行归一化处理，即要求在广义坐标空间下，对cTi中的c进行调整。令广义质量矩阵为单位阵，有：

归一处理后，主振型坐标系统下的动力方程可化为：

【程序实现】

（1）按静力分析模式，选择分析自由度，并形成结构刚度矩阵。

（2）按静力分析的单元形成单元质量矩阵；按单元定位向量集成结构质量矩阵。

（3）按质量矩阵进行矩阵凝聚。

（4）根据凝聚后的自由度计算特征对。

（5）变换回原始坐标系统。