式（6.19）是刚度矩阵相对于质量矩阵的广义特征值问题，其中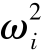和Ti为特征对。

1）代数方程求解方式

由于任一特征向量皆应非零，齐次线性方程式（式6.19），有非零解的前提是系数行列式为0，即：

式（6.20）为关于ω2的一元n次方程（n为动力自由度数目），称为频率方程，在质量矩阵和刚度矩阵已知时，可据此方程解出n个ω2的数值。

再将某一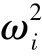回代，可进行对应Ti的求解。注意：回代后，线性方程（式6.20）的系数行列式为零，故无法求解（n个方程中只有n-1个方程线性无关）。但Ti仅为坐标变换需要的空间正交基向量，因此，求解时常设此向量第一个分量值为1，即可据此方程解出向量Ti。

从求解过程可知，cTi必然也是满足方程的解（c为任意非零实数）。在前述方程中解出的n列Ti，即可确定此时用于坐标变换的T矩阵：

2）矩阵求解方式

程序计算时采用矩阵算法进行。对于自由振动分析的广义特征值问题，方程改写为：

动力凝聚后的质量矩阵正定，故可用M-1乘上式两边，有：(www.daowen.com)

即将广义特征值问题转化为标准特征值问题。但M-1K并不一定对称，考虑到式（a）中质量矩阵M为实对称正定，总唯一存在一个可逆的下三角阵L[按式（1.1）进行Cholesky分解]，即有下式成立：

将式（b）代入式（a），有：

式（c）左右前乘L-1，有：

令LTT=A，并展开转置内容，可得：

再令

即对实对称的刚度矩阵K执行特定变换，保证变换后矩阵P的对称性，式（e）可表达为：

至此，广义特征值问题转化为实对称矩阵的标准特征值问题，可直接使用雅可比法解出矩阵P的特征值ω2。而特征向量A需要再做以下变换：

若质量矩阵皆为按集中质量矩阵形式集成时，因为质量矩阵为对角方阵，Cholesky分解可容易得到（即平方根法）：