动力自由度下的运动方程，根据矩阵元素的物理意义可知，质量矩阵可以是对角矩阵（按集中质量模式集成时），但刚度矩阵通常为非对角矩阵。

因此在原始坐标系统下（以下称为主坐标），按直接平衡条件所建立的微分方程中，各自由度相互耦合，难以直接分析，需作矩阵变换，执行解耦。

主坐标下位移向量表达为Y，在另一广义坐标空间内，位移向量选择不同的“基”，相同的位移量被表达为Q，位移向量在两个几何坐标之间的矩阵变换可表示为

式中　T——坐标变换矩阵。

将此变换代入主坐标系统下自由振动的运动微分方程，即可得

由于质量矩阵与刚度矩阵皆为主坐标系统下所得，显然此式仍为主坐标系统下关于惯性力和弹性恢复力的动平衡方程。

由逆步变换原理，式（6.11）成立时，还应有：

式中　FY——主坐标空间内的力向量；(www.daowen.com)

　　　FQ——广义坐标空间内的力向量。

利用式（6.13），将平衡方程式（6.12）中，惯性力MT（t）和弹性恢复力KTQ（t），变换至广义坐标系统下，形成在广义坐标系统下的平衡方程，即

此变换显然在任意的几何坐标变换下都应成立。其中：

TTMT：此矩阵最后将与广义加速度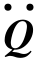（t）相乘，定义为广义坐标系统下的广义质量矩阵，用矩阵MQ表示。

TTKT：此矩阵最后将与广义位移Q（t）相乘，定义为广义坐标系统下的广义刚度矩阵，用矩阵KQ表示。

因此，广义坐标系统下的运动方程可写为：