1）集中质量矩阵

若“有分布质量”杆，其弹性变形对动力效应影响较小时，可将单元质量直接集中至单元结点自由度上，此时使用单元集中质量矩阵。质量集中到结点上时视为质点，并只计其在正交主轴方向上的平动，质点的转动质量此时忽略不计。

对于等截面平面杆元，分布线质量为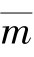，杆长为l，单元坐标系统下集中质量矩阵可表达为（不计转动惯量）：

此单元质量矩阵对应于图6.2所示的“一个单元”模式。若直接使用用质点简化方式，对分析精度产生较大影响时，可对单元进行细化处理。如图6.2所示，单元细化程度越高，质点分布越均匀，对原分布质量的代表性也越好。

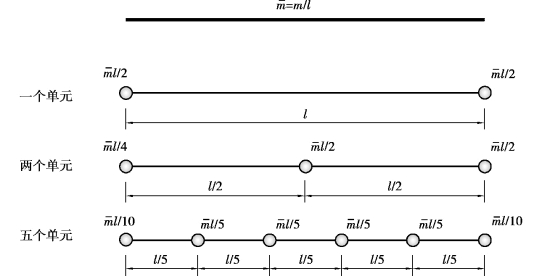
图6.2　集中质量简化时细化单元

2）一致质量矩阵

杆件的质量分布对动力响应影响较大时，仍采用图6.2的处理方式，细化到足够程度即可保证精度。但单元数目的增加，必然导致结构动力分析自由度数目过多，对后续分析非常不利。此时可在单元内部，考虑质量因弹性变形而产生的运动，即使用杆件的可能运动去描述分布质量对动力响应的影响（图6.3）。

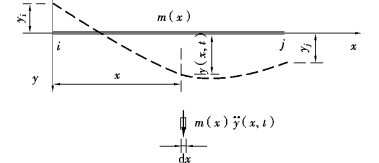
图6.3　动力效应与质量分布

若单元内部的位移分布和质量运动产生的惯性力皆相对均匀，可利用单元的位移插值函数N（x），通过结点动位移去表达单元内部的动位移分布。根据虚位移原理，分布惯性力在单元虚位移上所做虚功，应等于等效结点惯性力在单元结点虚位移上所做虚功，即根据“能量等效”原理进行以下推导。

下面是一维杆元的推导[m（x）为截面质量沿杆长的分布函数]。

①分布惯性力m（x）在单元内部设定虚位移分布y∗（x，t）上做虚功：。

②等效结点惯性力在结点虚位移δe∗（t）上做虚功：。(www.daowen.com)

③根据能量等效，并考虑有y∗（x，t）=N（x）δ∗，可得：

从上式中消去与积分无关的结点虚位移和虚加速度向量，即得：

式（6.5a）为杆单元一致质量矩阵的计算公式，应用于其他类型的单元时（如平面或实体单元），也可写为统一形式（此时ρ为密度分布函数）：

式（6.5）可将分布质量按设定的可能位移分布，“等效”变换到结点自由度上。

使用可能位移模式与有限元单元静力分析概念类似，详见第3章位移插值函数的相关叙述。位移插值函数通常会选用与静力分析一致的形式，称为一致质量矩阵（或协调质量矩阵）。由于运动的任意可能性，无法保证如静力分析一般，杆元设定的可能位移函数可由简单函数进行相对准确描述。即，一致质量矩阵通常只能是一种近似分析方法。

位移插值函数轴向位移描述选用式（4.9）（线性位移分布），切、弯向位移选用式（3.19）（三次多项式），平面等截面直杆的单元质量矩阵，可据式（6.5a）积分计算为：

普通框架结构动力分析时，由于质量主要集中于楼盖部分，又以水平运动为主（地震荷载、风荷载），单元内部的弹性变形对结构动力效应影响较小，一致质量矩阵对模型计算精度的提高意义一般不会太大，故常规杆系结构分析时仍会选择集中质量矩阵进行计算。但若分析对象为“空旷、大跨”，没有明显占优的集中质量分布于结点时，杆件弹性变形对结构动力效应影响明显。选择一致质量矩阵，可在一定程度上提高动力分析精度。

【程序实现】