空间结构自由度等效变换的原理和平面结构相同，下面仅对刚性楼层的几何变换进行讨论。

刚性楼层是框架结构分析较常使用的工程设定。结构楼面面积通常较大，在考虑结构板在楼面运动自由度间的束缚作用后，各结点楼层平面内的相对位移一般可以忽略不计。分析楼面结点，在该平面内拥有完全相同的3个运动自由度（平面外的另3个运动自由度仍各自独立），由于平面刚体的转动效应，各结点自由度相同，但位移值却不同，如图5.21所示。由此产生了自由度在刚性平面内的空间旋转变换问题。

图5.21　刚性楼面设定

在设定的刚性平面内选取任一结点作为分析楼面运动的主结点，以此主结点自由度代表楼面内所有结点“在平面内”的自由度，被代表了自由度的结点皆称为其从结点。

以下变换关系中，设定刚性平面位于XOY平面，即正交于Z轴。对于斜楼面，几何变换矩阵还需要在空间坐标系统下进行二次变换。

刚性平面位于XOY平面内时，按本书所采用坐标系统的坐标分量约定，刚性等效变换对应于结点在整体坐标系下第1、2、6自由度，即u，v，ϕZ。由于刚性楼面涉及的关联结点数目较多，而先处理法自由度编码无规律可寻，本知识点讲解内容只按后处理法方式作介绍。先处理法也可依照此原理进行，只是编程实现时定位关系会复杂一些。

如图5.22所示，以结点i为楼层平面内主结点，结点j（k等）为其从结点，主从自由度关系可直接根据结点号确定。其中，i可在不同楼层定义不同的主结点，仍有相应的j（k等）可与之关联。i、j为原始状态，i′、j′为位移发生后状态。

图5.22　刚性平面内主、从结点的自由度变换

根据图5.22（a）所示，主从自由度变换关系可由下式确定：(www.daowen.com)

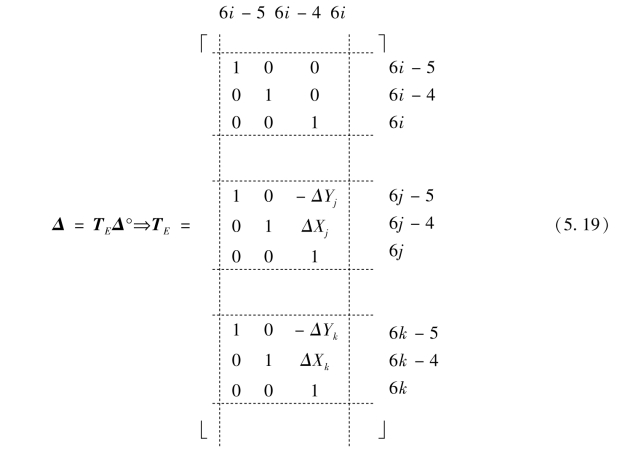
ΔX和ΔY为主、从结点在整体坐标系统下平面内位置的相对关系，可根据结点整体坐标值计算：

式中，上标MJ，为主结点坐标；上标SJ，为从结点坐标。

【程序实现】

刚性楼层假定时，矩阵TE的程序实现如下：

（1）根据结点数m，形成单位阵I（6m×6m）。

（2）在每一楼层，确定一个主结点i，并将归属于本楼层的其余结点定为从结点。

（3）根据式（5.19），对矩阵列6i-5、6i-4、6i，分别对所有从结点号j的对应行6j-5、6j-4、6j进行修正。

（4）所有楼层修正完毕后，划除所有楼层、所有从结点号j的对应列6j-5、6j-4、6j，即可形成TE。