除置大值方式外,还可采用绝对刚性设定,即通过关联自由度间的几何变换矩阵实施等效。但需注意:绝对刚性设定下,刚性单元的某些杆端位移分量,必然对应于刚体运动。即意味着不存在相关变形,此单元在相应自由度方向上,将不存在对应于弹性变形的内力解答。
具体处理方式:单元分析时,仍正常形成单元刚度方程,自由度的等效关系在结构刚度方程集成时或集成后再行修正。本方式实现的是相关联自由度间的真正等效,从力学概念上保证绝对刚性,可有效减少分析自由度,更适用于大型结构分析。
1)指定位移编码相同(先处理法)
根据结构整体变形特征,先处理法可直接指定整体分析时某些自由度对应的未知量相同,在结构刚度方程集成时实现一些特定自由度等效。
如图5.15所示,因轴向变形忽略,任意荷载作用下,结点2、3、4的水平位移值必然相同,在结点位移编码时,设定对应的结点位移自由度为同一编码(2)。整体分析时将不计相应单元(②、④)的轴向刚度特征。
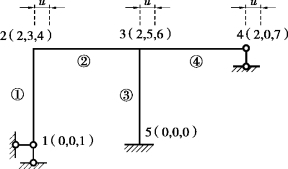
图5.15 先处理法对自由度等效的处理
先处理法对位移编码的处理有明显的局限,仅能处置对应于整体坐标系统下平动自由度的直接等效关系。
2)几何矩阵变换(主从自由度)
几何矩阵变换方式可令模型中矩阵分析概念更清晰,在结构通用分析时更为实用。
首先,对“先处理法指定位移编码相同”的变换方式(即上面的方法1),将其解释为矩阵变换形式。
平动等效自由度属于整体坐标系统时,即对应于先处理法设定位移编码相同的适用模式中,结构分析时有刚度方程:
![]()
整体分析时,设定约束条件(如某结构分析时,2、3自由度平动等效)为:
![]()
现以原始几何空间内位移向量为Δ,因约束等效变换后的几何空间内位移向量为Δ°。
对刚度方程进行矩阵子块划分。其中,下标1对应的子块,为未设置等效要求的其他自由度集合;2、3自由度则为等效自由度。刚度方程表示为:
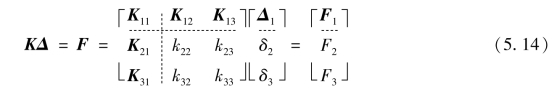
根据位移向量的等效性,位移向量在两个不同坐标空间的变换可写为TE,称为几何等效变换矩阵,位移向量在两个空间有以下几何变换关系:
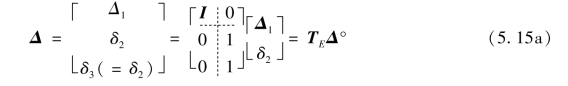
显然,若有多个自由度皆对应等效于δ2时,式(5.15a)可扩展写为:
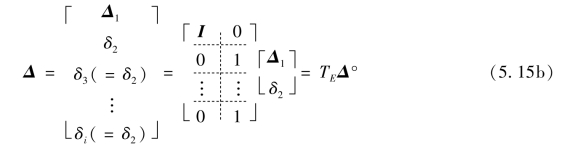
此时取δ2为主自由度,因约束等效与主自由度相同的位移分量(δ3,…,δi),皆为其从自由度。平动自由度等效时,对应自由度作用结点力的作用效应,可直接叠加(自由度为共线模式,至于不共线且还等效的自由度,模型过于理想化,在此不作描述)。
力向量在两个不同坐标空间的变换写为:
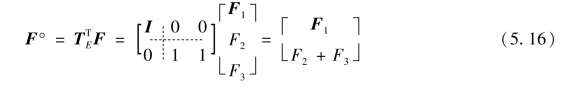
可见,式(5.15)和式(5.16)仍满足逆步变换原理。
根据力变换式(5.16),对式(5.14)左乘变换矩阵 ,将结点力向量变换至主结点向量空间,表达为:
,将结点力向量变换至主结点向量空间,表达为:
![]()
再将位移向量变换式(5.15)代入式(a),可得:
![]()
式(5.17a)可展开写为:

【例5.5】如图5.16所示的平面刚架,若横梁不计轴向变形,试根据自由度几何变换的概念集成结构刚度方程。各杆E、I、A、l均为常数。
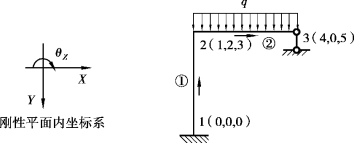
图5.16 自由度等效示例
【解】(1)单元分析。
单元①:

单元②:

(2)按先处理法集成结构刚度方程:
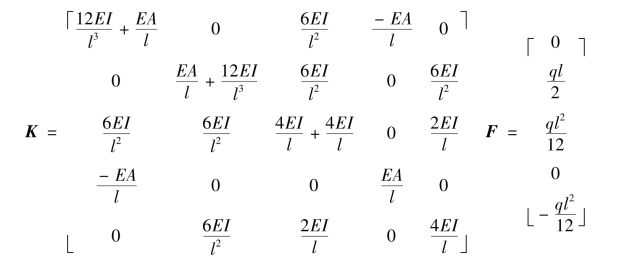
(3)单元轴向刚度无穷大,对应于结构坐标系下1、4自由度等效。以1为主自由度,4为从自由度,按式(5.17b)对结构刚度矩阵和荷载列阵修正如下:

【说明】
根据变换过程和结果可知:
(1)几何坐标变换方式,与先处理法结点位移编码方式一致,仍是处理整体坐标系统下的等效平动自由度,只是将分析过程解释成为矩阵变换。
(2)几何变换方式,可方便扩展至任意平动方向、或转动方向。
(3)特别注意,主从自由度方向若存在刚性外约束,由于先处理法约束处自由度已经缺失,几何变换中自由度的对应关系可能会现出错。为避免此情况,可尽量使用后处理法。即便使用后处理法,也应注意约束引入,是否与几何变换时的自由度对应关系相冲突,本书不再对此继续讨论。
3)等效平动自由度位于任意指定方向时的几何变换
如图5.17所示,若斜杆ij轴向变形忽略不计,或在结点间直接指定两点连线方向自由度等效关系时(如刚性支撑ij)。此时自由度的等效关系不能由结构坐标系统下的自由度进行直接定义,变换方式可作以下修正。
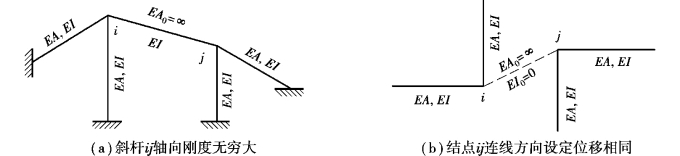
图5.17 非整体坐标上平动自由度等效
几何变换关系以图5.17(a)的模型为例,说明如下。
斜杆ij轴向刚度无穷大,抗弯刚度为常量,未作等效变换的结构刚度方程仍写为:
![]() (https://www.daowen.com)
(https://www.daowen.com)
小变形平动等效变换时,不涉及转动自由度,且由于轴向变形忽略不计,关联于本单元ij的4个平动自由度中,仅有3个为独立分量,自由度间的几何关系如图5.18所示。
如果设定vj非独立,即:
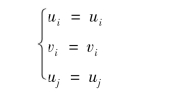
根据图5.18所示几何关系,显然有:
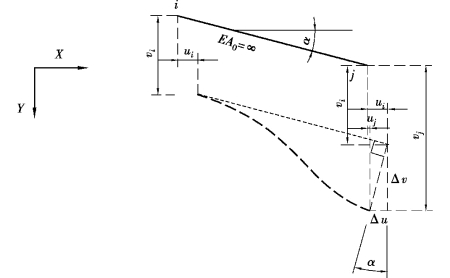
图5.18 平动自由度等效的几何关系
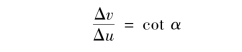
可表达出:
![]()
几何变换关系可表达为:
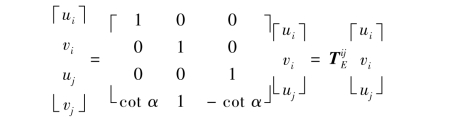
为避免正切(余切)函数的无穷大取值,如果单元在整体坐标系统下的方向角α接近0°或180°时,变换关系调整为:
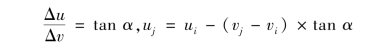
即

结构整体自由度的几何变换矩阵则可写为:

4)完全刚性杆对应的自由度等效
平面杆系结构中,因不计轴向、弯曲变形,刚性杆单元自由度等效的几何变换关系如图5.19所示。
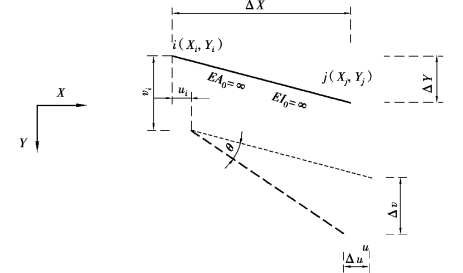
图5.19 转动时关联自由度间的几何关系
图5.19中,结点i、j以刚性单元相连,单元只存在3个独立自由度,利用始端结点自由度表达末端结点自由度,末端位移增量可用始末端结点间坐标差值(即单元长度的水平、竖向投影),与单元转角之间的乘积表达。关联自由度间存在以下坐标变换:
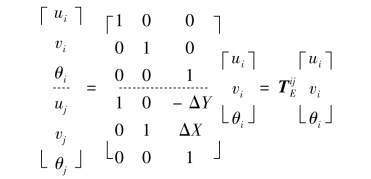
而结构整体自由度的几何变换矩阵则可写为:

显然,经TE的几何变换,将从结构刚度方程中消去刚性单元末端对应的3个自由度,此几何变换矩阵仍非方阵。
5)整体分析
根据所设置内部束缚条件对应的几何特征,构建几何等效变换矩阵TE。通过TE联系两个向量空间内的结点位移向量和结点力向量:
![]()
如平动、转动、刚体等效等几何变换关系,都可合并至TE矩阵中,集中表达自由度之间的直接几何关系。因变换过程存在必然的自由度缩减,几何等效变换矩阵皆非方阵。自由度等效变换后的结构刚度方程为:
![]()
其中
![]()
【程序实现】
(1)依据式(5.18)原理,建立自由度间的几何等效变换矩阵TE,利用TE变换结构刚度矩阵(或原始刚度矩阵):
![]()
(2)利用TE变换力向量:
![]()
(3)解方程,再由Δ=TEΔ°,可获得位移的完整解。
【例5.6】试用后处理法+几何变换方式,形成如图5.20所示结构的结构刚度矩阵。
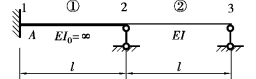
图5.20 例5.6图
【解】(1)采用后处理法,EI0取为任一常量。根据刚度系数的物理意义,直接形成结构刚度矩阵,两个模型的结构刚度矩阵皆可表示为一致的形式。
单元①、②单刚写为:
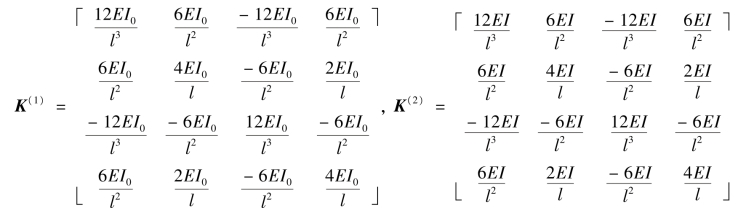
(2)原始刚度矩阵集成为:

(3)建立几何等效变换矩阵。
以自由度1、2为主自由度,3、4为其从自由度,5、6为独立自由度,可得:
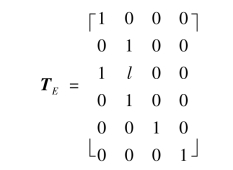
(4)利用几何等效变换矩阵,对原结构刚度矩阵执行变换:
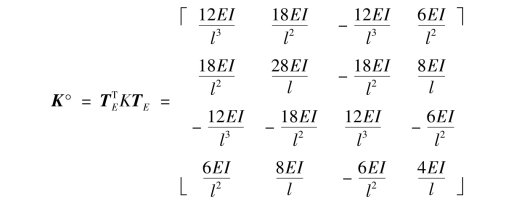
变换后,所有EI0对应的刚度系数都会从整体刚度矩阵中消除。
(5)主一副0形成结构刚度矩阵:
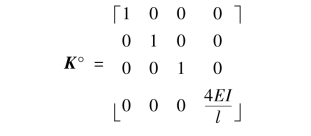
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







