【摘要】:图5.12弹性支座处理刚度系数增加弹性支座后的刚度系数,可根据定义直接实现。弹性支座对应自由度上发生单位位移时,所需要施加力的大小即为此自由度对应的刚度系数。容易知道,修正结构刚度矩阵时,在对应于弹性支座自由度处的刚度系数kii,附加上弹性支座的刚度系数k弹即可。按刚度系数定义,直接写出结构坐标系统下的结点刚度矩阵:根据式,在第1自由度对应的主元素上,叠加弹性支座刚度系数,有:
支座刚度通常远大于上部结构刚度,在大多数结构中,支座约束效应按无限刚性进行简化计算,是可行且有效的。但若支座刚度较结构刚度并不完全占优时,便需要在受力分析时考虑支座变形的影响,此时需要引入弹性支座。
弹性支座对结构分析方式的影响体现在以下两个方面:
(1)未知量数目
先处理法中,刚性支座约束对应的结点位移编码为0,不存在未知结点位移;但弹性支座存在时,在弹性约束方向,显然会产生未知位移。因此,应在此自由度方向上增加位移编码。
后处理法不需要处理结点位移编码,在引入支座约束时,不去修正弹性支座对应自由度即可。
如图5.12(a)、(b)所示,结构中的结点3因不同的约束状态,在结构位移编码上存在差异(对应于先处理法)。

图5.12 弹性支座处理
(2)刚度系数
增加弹性支座后的刚度系数,可根据定义直接实现。(https://www.daowen.com)
弹性支座对应自由度上发生单位位移时,所需要施加力的大小即为此自由度对应的刚度系数。容易知道,修正结构刚度矩阵时,在对应于弹性支座自由度处的刚度系数kii,附加上弹性支座的刚度系数k弹即可。
若弹性支座对应的自由度为i,则有:
![]()
【例5.4】试以先处理法建立图5.13所示结构的结构刚度矩阵。转动弹性支座的刚度系数k弹=EI/l。

图5.13 例5.4图
【解】(1)弹性支座对应自由度同样进行结点位移编码。按刚度系数定义,直接写出结构坐标系统下的结点刚度矩阵:

(2)根据式(5.13),在第1自由度对应的主元素上,叠加弹性支座刚度系数,有:
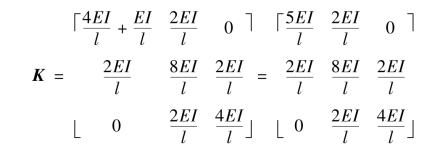
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章








