考虑结点区域刚域影响时，带刚域单元的结点自由度与弹性端自由度之间，显然不再相互独立。如图5.10（a）所示，单元总长为l，其中弹性部分长度为l0，始末端刚域长度分别为a、b。以下分析中，弹性段各物理量均带下标“0”作为标志。

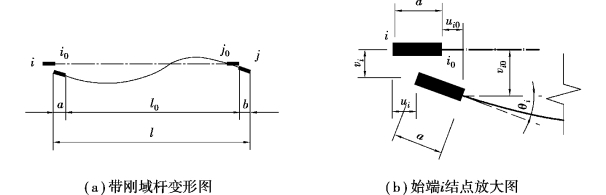
图5.10　带刚域杆单元的始端结点自由度变换

单元分析首先是建立在弹性段的基础上，而结点自由度与弹性部分端点自由度的关系则根据几何变换确定。

1）始端结点分析

在始端结点分析的位置，自由度的几何变换关系如图5.10所示。

根据图5.10（b）所示的几何关系，i0端结点自由度可由i端自由度表示如下：

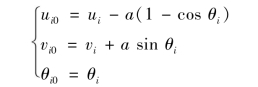
小变形时，θ≈sinθ，而1-cosθ=2sin2（θ/2），此高阶无穷小在小变形时忽略，故上式简化为：

整理成变换矩阵形式，有：

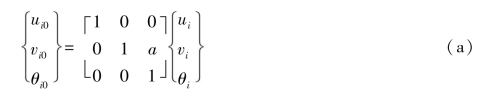
2）末端结点分析(www.daowen.com)

在末端结点的位置，自由度的几何变换关系如图5.11所示。

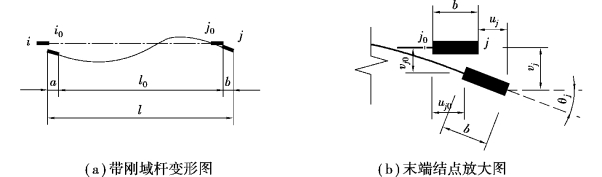
图5.11　带刚域杆单元末端结点自由度变换

根据图5.11（b），j0端结点自由度可由j端自由度表示如下：

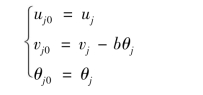
整理成变换矩阵形式，有：

3）结点几何变换

合并几何变换矩阵（a）、（b），可在两个广义坐标系统（刚性端自由度-弹性端自由度）之间建立如下几何变换关系：

其中：