【摘要】:此时单元杆端力可据式(5.6)的原理,在被释放自由度的单刚方程中进行计算。②确定需要释放的整体坐标系统下单元自由度位置,利用单位阵划列取得矩阵子块元素的数据传送矩阵:③可从原单刚中取得计算所需的各子块:④自由度释放的单刚和固端力根据公式计算:⑤单元和整体自由度间的数据传送矩阵,同样剔除被释放自由度,做划列处理。
自由度释放是在单元分析完成之后,在形成结构整体刚度方程之前,故先后处理法皆可使用其引入衍生单元。先处理法经自由度释放后,可不再考虑内部结点的特殊约束,只需要按特殊结点信息引入支座约束;后处理法经自由度释放后,便可由主1副0、乘大数法等引入支座信息。
比较图5.4和图5.5,可知无论是先处理法还是后处理法,经过自由度释放后,未知量数目在整体分析阶段都可得到有效减少。
被释放的自由度不参与结构的整体分析,结点位移向量求出后,将不会包括被释放自由度的位移值。此时单元杆端力可据式(5.6)的原理,在被释放自由度的单刚方程中进行计算。也可根据式(1.19),用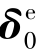 表达出
表达出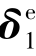 后
后![]() ,再合并
,再合并![]() ,得到完整单元自由度相关解,最后利用一般杆元的刚度方程进行计算。
,得到完整单元自由度相关解,最后利用一般杆元的刚度方程进行计算。
【程序实现】
①形成各单元单刚,并变换至结构整体坐标系统下。
②确定需要释放的整体坐标系统下单元自由度位置,利用单位阵划列取得矩阵子块元素的数据传送矩阵:

③可从原单刚中取得计算所需的各子块:

④自由度释放的单刚和固端力根据公式计算:
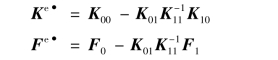 (https://www.daowen.com)
(https://www.daowen.com)
⑤单元和整体自由度间的数据传送矩阵,同样剔除被释放自由度,做划列处理。
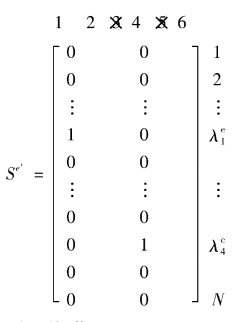
可借用子块传送矩阵S0实现划列操作:
![]()
⑥形成结构刚度方程,求解出结点位移向量Δ,再执行![]() ,可取得对应于本单元释放自由度后整体坐标系统下的单元杆端位移向量
,可取得对应于本单元释放自由度后整体坐标系统下的单元杆端位移向量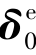 。
。
⑦由式![]() ,取得被释放自由度的杆端位移。
,取得被释放自由度的杆端位移。
![]()
⑧合并形成单元的完整自由度解单元坐标系统下的杆端力向量可表达为:
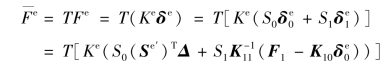
对应于自由度释放的刚度方程集成部分程序段如下。(未再列写单元杆端内力计算程序段,读者可据前述公式编写)

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章





