平面杆系结构分析时，根据杆端位移描述的需要，使用两结点六自由度的一般杆单元。一般杆元通用程度高，但在前处理时，若体系中存在非全刚性结点，因结点无法位移完全协调所有的杆端位移，所以按矩阵位移法中介绍的思路，先处理法需要进行“重结点”编号。后处理法的处置方式也与先处理法类似，即增加一个“过渡单元”去连接不协调的杆端位移，如图5.4所示。

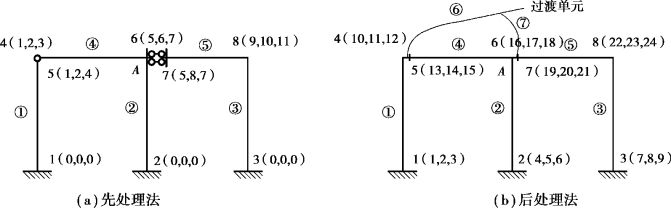
图5.4　重结点编号处理特殊结点

“重结点”编号模式中，结点编号需要人工干预。如果重结点数目较多，会产生较大的数据前处理工作量。在实际工程分析时，结点编号和单元编号都是由系统自动生成的，引入重结点编号并不方便。

注意到经典位移法计算时，曾根据杆端力的特征使用衍生单元（两端固端的杆单元为一般单元；而一端固端、一端铰结的单元，或一端固端、一端定向的单元，这两类单元是在一般单元的基础上衍生出来的，本书称其为衍生单元），若可使用衍生单元，则非协调于结点的杆端自由度不再纳入体系整体分析，就自然不再存在结点位移与杆端位移的非协调问题。(www.daowen.com)

但直接引入衍生单元仍不可取，因为基本单元类型增多，同样会让前处理难度加大。

更好的方式是将非全刚性结点模式的内约束，由结点处理模式转换为单元内部处理。在单元分析完成后，对单元实施自由度释放，此时所有存在的非协调于结点的杆端位移，皆视为“非独立”未知量予以释放，释放后的自由度不再参与整体分析。这样能保证结点位移与杆端位移完全对应，结点位移可有效表达杆端位移。

如图5.4中所示结点和结点自由度编码位移编码，在“非独立自由度”（图5.5所绘出的指定自由度）不计时，可变换成图5.5所示的模式。经此处理，单元杆端和结点之间的对应关系可得到简化。

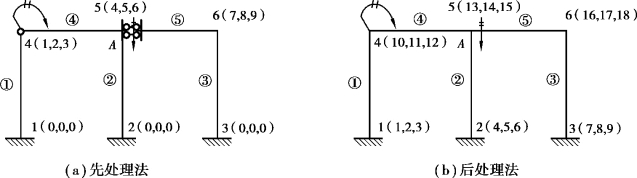
图5.5　自由度释放后的结点与位移编码