1）后处理法的基本概念

对于所有结点均为刚结（或经处理后视同为刚结）的杆系结构，可使用后处理法引入支承约束条件。后处理法对所有结点（也包括支座结点），直接按结点编号顺序，自动形成结点位移编码，在此阶段暂无须考虑任何约束信息。

对于第i结点，结点位移编码由对应结点号自动形成：

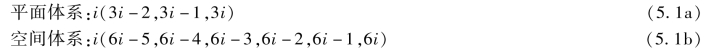
后处理法集成的整体刚度方程，用结点号为索引，以矩阵子块形式写为：

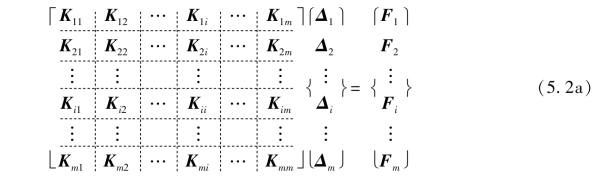
式中　Kii——对应于结点号i的矩阵子块，为3×3子矩阵（空间体系为6×6）；

　　　Δi——结点号i对应的三个位移分量（空间体系为6个分量）；

　　　Fi——结点号i对应的三个综合结点力分量（空间体系为6个分量）；

　　　m——体系的总结点数，未知量数n=3×m（空间体系n=6×m）。

式（5.2a）也可展开，表达为：

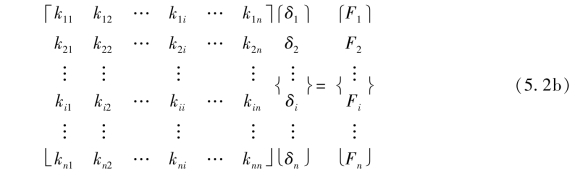
根据单元对应的始末端结点编号（集成方式仍类同于先处理法，结点位移编码直接与结点编号对应，不用单独存储），可集成刚度方程。本阶段集成时，后处理法未引入支座约束条件，所集成的刚度方程对应无支承的“自由”结构。不包含支座约束信息的刚度方程，称为结构原始刚度方程（式5.2），其对应的刚度矩阵称为原始刚度矩阵，原始刚度矩阵通常为奇异矩阵。进行方程求解前，还需要根据外部约束，引入支承条件。

2）后处理法支座约束的引入

在后处理法中，只需要引入外约束条件，特殊结点信息内容更为精简，特殊结点信息数组同第5.1.1节方式。根据输入的特殊结点信息，用于引入支承条件的方法有主1副0法、乘大数法、划行划列法（矩阵凝聚法）等。

（1）主1副0法

根据结构的支承条件，在刚性约束处，结点位移分量已知：δi=ci（ci=0；或ci≠0时，对应于已知支座移动），故将K中第i行的主元元素改为1，将第i行、第i列的其他副元元素均改为零；同时将F向量中第i个分量Fi改为ci，并对自由项其他分量作相应修改。

对第i自由度使用主1副0法，引入支承条件后刚度方程修改为：

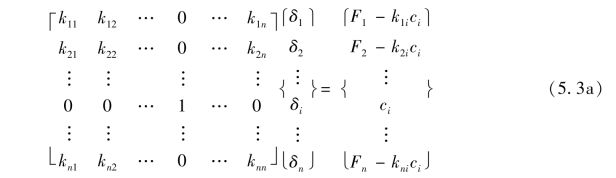
根据式（5.3a），对第i个方程，即可解出：

若支座移动以单元广义荷载方式引入，即取式（5.3a）中ci=0。此时刚度方程的修改如式（5.3b）所示：

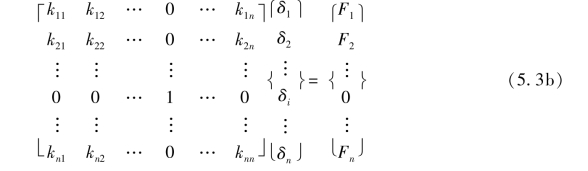
（2）乘大数法

将原始总刚K中对应于支座约束第i自由度的主元元素，乘上一个充分大的数V（如可取V=108~1020，即本自由度的主元数值相对于本行、列所有副元元素，占绝对优势）。同时，将F中的第i分量Fi，修改为V·kii·ci（ci=0或ci≠0）。

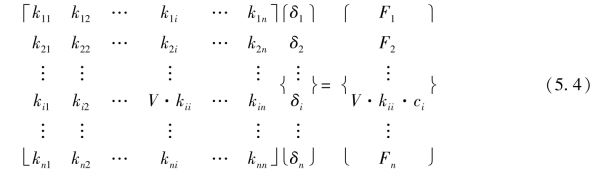
乘大数法与主1副0法[式（5.3a）]相比较，方程中修改项少，有、无支座移动的修改模式一致，故应用更简便。

（3）划行划列法（矩阵凝聚法）

也可用划行划列法（矩阵凝聚法）对有支座约束的原始刚度方程进行计算。

划分结点位移向量子块，取：

式中　Δ0——对应于结点的未知位移分量；

　　　Δ1——对应于支座约束处的位移分量。

式（a）可按以下两种情况进行分析：(www.daowen.com)

①若无支座移动发生（或将支动移动视为广义荷载引入），则Δ1=0，为零向量；

②若有支座移动发生，则Δ1为非零向量。

具体分析如下：

按已知、未知自由度，对结构原始刚度方程进行子块划分，有：

情况①中，取Δ1=0，则式（b）变换为：

引入支座约束时，支座约束对应的自由度可视为无效自由度。即将原始刚度方程中，所有对应于支座约束的行、列划除（如式5.5中，第i自由度对应于支座约束），矩阵缩聚的方法被形象地称为划行划列法。直接划除行列时，支座位移应以广义荷载的方式引入。

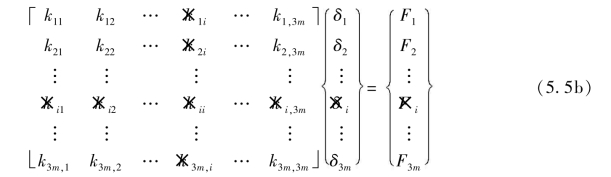
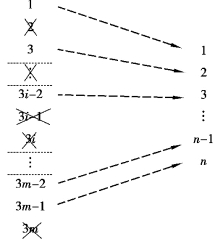
图5.2　划行划列时自由度索引关系

由式（5.5）可知，划行划列法是在原始刚度方程中，直接划除刚性外约束自由度的所有影响，从而得到未知量和方程阶数皆与先处理法相同的结构刚度方程。

划行划列后，结点号与位移编码再无直接对应关系（图5.2），需要对位移编码进行重新编号、索引（向量空间从原3m维度缩减至n维；自由度索引可在整体向量空间上设定传送矩阵S实施）。划行划列法的处理环节，是在结构整体刚度方程形成之后，仍归入后处理法，但从最后自由度编码和所形成的结构刚度矩阵来看，又类同于先处理法，程序整体分析在方程求解及之后的内容，也与先处理接近。

对于情况②，支座约束对应的Δ1为非零向量，可进行矩阵凝聚。具体做法是根据式（b）并结合式（1.20）即可完成。完整的矩阵凝聚可以直接引入非零支座移动，但需要处理矩阵求逆。

3）后处理法特点

与先处理法相比较，后处理法最为明显的特点是无须处理结点位移编号（矩阵凝聚时除外）。尽管未知量数目更多，矩阵存储空间和结构刚度方程求解的计算量也相应增加，但程序编写显然会更为简洁。

后处理法的其他特点还包括：

（1）体系未知量不同

先处理法以未知结点位移为基本未知量；后处理法以所有结点位移（含支座已知位移）为基本未知量。故后处理法未知量数目更多，线性方程求解过程中计算量会更大一些。若因采用后处理法使得计算量较先处理明显过大时，仍可采用矩阵凝聚的方式（约束较多的大型结构复杂工况分析时可考虑），缩聚线性方程。

（2）支承引入阶段不同

后处理法是在整体刚度方程集成后，再引入支承条件。

（3）内约束处理方式不同

后处理法无法对内部结点约束进行直接修正，只能用于内部结点均为一般刚结（或经处理后视同为刚结）的体系。

4）后处理法对特殊结点的处理

结构不可避免会存在特殊结点，后处理法对特殊结点的处理方式有以下两种方式。

（1）利用过渡单元模拟特殊结点

铰结点模式：如图5.3所示，增加了结点5和单元③，以模拟铰结点的性能。此时的单元③为过渡单元，在单元参数输入时，应尽量模拟出“铰”的性能，即要求过渡单元长度小、轴向切向刚度近无穷大、转动刚度近于0。

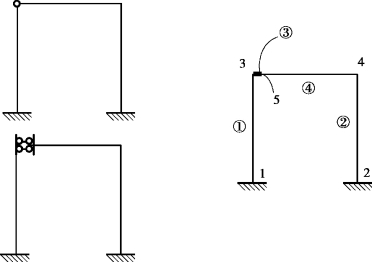
图5.3　过渡单元（单元③）模拟特殊结点

定向结点模式：采取如铰结点相同的处理模式，增设单元模拟定向结点的性能。此时的单元性能要求是过渡单元长度小、轴向刚度近无穷大、转动刚度无穷大、切向刚度近于0。

（2）自由度释放，引入特殊杆单元

过渡单元始终无法完整模拟特殊结点的性质，所以必然会产生误差。同时，过渡单元还需要人工干预结点、单元，对前处理效率影响较大。

使用有限元分析处理特殊内约束，通常通过释放单元自由度进行。单元自由度释放是一种通用方法，在先、后处理法中皆可使用，详见下一节。