在FEA的子程序EFF中，使用变换矩阵直接获取等效结点荷载向量，而非MDA中所计算的单元固端力，需要应注意与矩阵位移法载常数的区分（二者相差一个负号）。在有限单元分析模式下，EFF等效结点荷载计算方式分为三种模式、七种类型，本节中荷载作用位置参数均按相对长度输入。

①单元集中力模式，输入格式：

单元号，类型（1、2、3），荷载值，位置参数

按集中力是轴向（类型一）、切向（类型二）还是力偶（类型三），从式（4.27）中取出对应的行向量作为N_S。

②单元分布力模式，输入格式：

单元号，类型（4、5、6），荷载值，作用起点，作用终点，函数类型

按分布力是轴向（类型四）、切向（类型五）还是力偶（类型六），从式（4.27）中取出对应的行向量作为N_S。

③温度等效荷载模式，输入格式：

单元号，类型（7），上侧温变值，下侧温变值，热膨胀系数，截面高度，上部温变函数类型，下部温变函数类型，截面高度变化函数类型

T_s为截面温度变形向量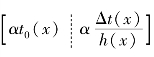

【例4.5】如图4.25（a）所示为一钢筋混凝土鱼腹式吊车梁，截面宽为0.3m，端截面高0.4m，跨中截面高0.8m，截面高度沿跨长为二次曲线变化。试以FEA程序计算跨中截面挠度。

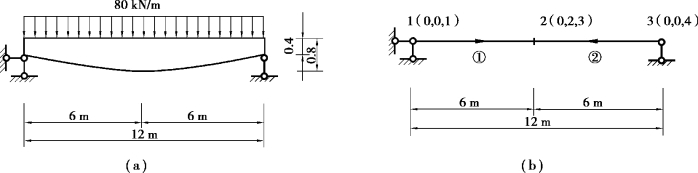
图4.25　鱼腹式吊车梁立面图及计算模型

【解】（1）为取得跨中截面挠度，在跨中截面增加一个结点，将结构拆分为两个单元分析，模型如图4.7.1（b）所示。在各单元始端结点建立坐标系统。为统一两个单元的截面刚度变化函数，单元②的坐标系统以3结点为始端。

（2）截面面积和惯性矩函数可写为：

截面高度为二次多项式变化，截面面积写为二次多项式：

截面惯性矩为六次多项式，自定义函数只支持三次多项式，故仍以三次多项式近似拟合为：

（3）输入数据文件的基本格式为：

（4）经计算，输出文件中位移和内力为：(www.daowen.com)

可得跨中截面挠度值为0.072m。

【例4.6】如图4.26（a）所示为一等截面简支刚架，其上作用各类分布荷载。试以FEA程序绘制弯矩图。

【解】（1）根据荷载特征，计算荷载函数取为：

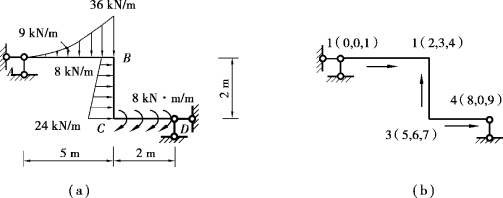
图4.26　等截面简支刚架图及计算模型

（2）计算模型如图4.26（b）所示，数据文件内容为：

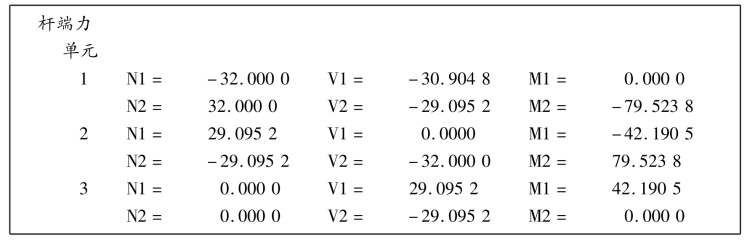
（3）经计算，输出结果文件为：

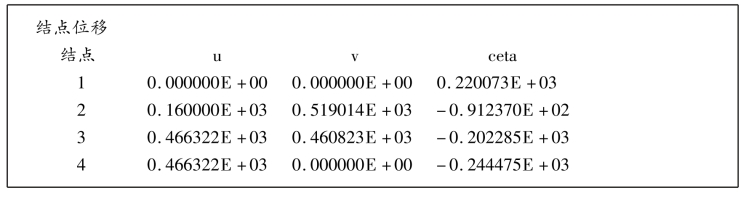
（4）内力图如图4.27所示。线性分布荷载对应的剪力分布为二次曲线，弯矩分布为三次曲线；二次荷载对应的剪力分布为三次曲线，弯矩分布为四次曲线。图中并未准确给出二次多项式以上内力曲线，仅作示意。若需要更准确获取内力分布，可细分单元，取得更多的控制截面内力值。

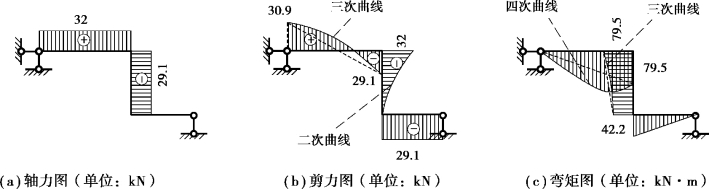
图4.27　内力图

【例4.7】如图4.28（a）所示的悬臂钢柱（Q235），截面形状特征和温变（沿柱高线性变化）如图所示。试以FEA程序计算温变下的顶点侧移值。热膨胀系数α=0.00001。

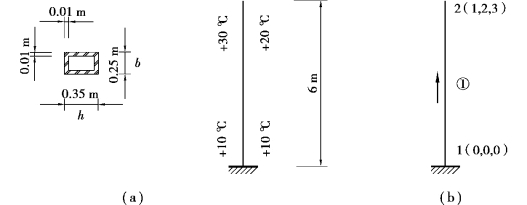
图4.28　例4.7图

【解】（1）取E=2×108kN/m2，根据截面参数计算可得A=0.047m2，I=0.0002044m4。

左侧温变，从下至上：t1（x）=10+3.333x

右侧温变，从下至上：t1（x）=10+1.667x

（2）计算模型如图4.28（b）所示，数据文件为

（3）输出结果文件为：（静定结构无内力）

可知顶点侧移值为1.7mm。