根据荷载向量的分量可知，荷载向量在截面的轴向、切向和转动位移方向上皆存在做功的可能，故应根据结点自由度，对截面在3个位移方向上的位移函数进行描述。

根据桁杆单元的位移插值函数，可得轴向位移插值函数为：

根据梁单元的位移插值函数，可得切向位移插值函数为：

还需要补充杆端自由度与截面转角位移之间的插值关系。由于截面转角为切向位移的一次导数，故可取：

合并以上三式，即可得：

【例4.2】某平面梁上作用单元荷载为竖向集中力FP，位置参数如图4.22所示，试计算其等效结点荷载。设定位移插值函数按仅考虑弯曲变形梁的位移插值函数选用。

【解】（1）因只存在切向荷载，所以位移插值函数取为：

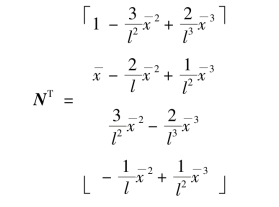
（2）由式（4.25）得：(www.daowen.com)

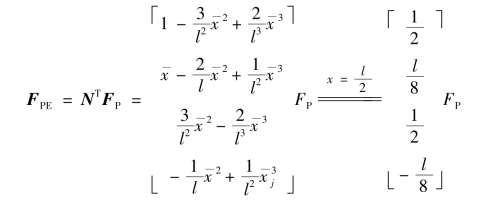
【例4.3】某平面桁杆上作用分布荷载q（x），函数关系和位置参数如图4.23所示，试计算其等效结点荷载。位移插值函数按桁杆位移插值函数式（4.27）选用。

图4.22　计算梁等效结点荷载

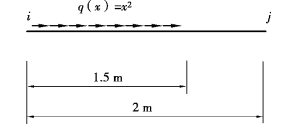
图4.23　计算桁杆等效结点荷载

【解】（1）位移插值函数：

（2）由式（4.26）得：

【程序实现】

以平面杆单元上作用横向分布荷载为模型，C为荷载函数系数（若设荷载沿杆长变化为三次多项式，即Q=C1x3+C2x2+C3x+C4），a、b为荷载函数作用区域，也即积分上下限；N_S为截面位移插值函数，对应于式（4.27）中第二行。