【摘要】:平面交叉梁系的分析对象一般为空间框架结构中的楼盖部分。图4.19平面交叉梁系的单元自由度在单元坐标系统下,对应的杆端力向量和杆端位移向量中,分量为:1)截面刚度关系在单元坐标系统下,考虑扭、弯变形时,截面的有效变形包括相对x轴的扭转变形和相对工程轴y轴的弯曲变形分量。
平面交叉梁系的分析对象一般为空间框架结构中的楼盖部分。由于楼面板的约束效应,结构在楼层平面内具有较大的刚度,梁在楼层平面内受到板支撑后,平面内的刚度可视为无限大。因此,楼盖分析时可只考虑梁单元在楼层平面外的位移和变形。
在如图4.19所示的整体运动坐标系统下,描述杆件平面外运动自由度的分量包括绕X轴的转动φx、绕Y轴的转动ϕy和沿Z轴的竖向位移w,如图4.19(a)所示。
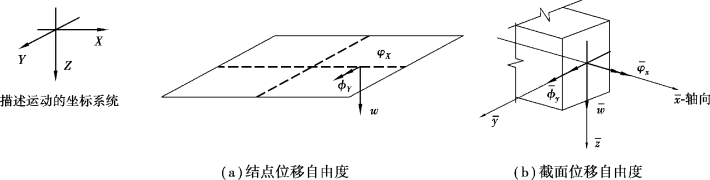
图4.19 平面交叉梁系的单元自由度
在单元坐标系统下(Z轴与z轴重合),对应的杆端力向量和杆端位移向量中,分量为:
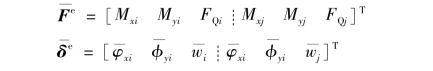
1)截面刚度关系
在单元坐标系统下,考虑扭、弯变形时,截面的有效变形包括相对x轴的扭转变形和相对工程轴y轴的弯曲变形分量。
平面交叉梁系中单元截面变形向量表示为:
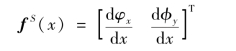 (www.daowen.com)
(www.daowen.com)
有效截面力向量包含两个对应分量——截面扭矩、相对工程轴y轴的截面弯矩,表示为截面力向量为:
![]()
截面刚度关系可由截面弹性矩阵表达为:
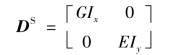
2)位移、变形分布函数
平截面假定适用时,截面扭转变形与弯曲变形,仍相互独立。扭转变形分布沿杆长为线性函数,参照轴向变形可取得;弯曲变形分布则据根据式(4.17)获取。注意:应根据结点自由度和截面变形的对应关系,重新整理项次排列关系。结点位移与截面变形之间的变换矩阵可写为:
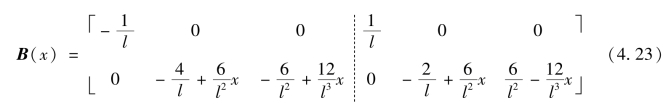
3)单元刚度矩阵计算
将B和D代入式(3.14b),可得:
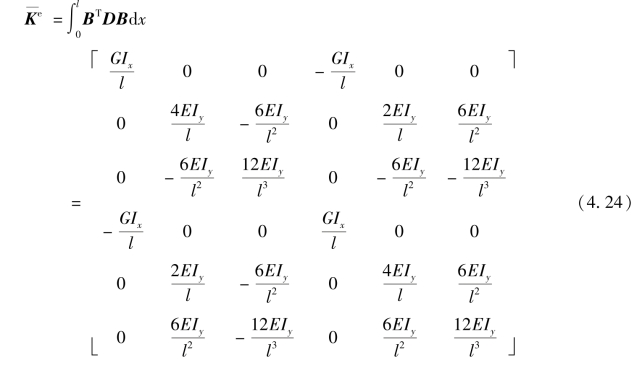
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关杆系结构有限元的文章







