1)截面刚度关系
截面的有效变形包含剪切变形和弯曲变形,如图4.13所示。
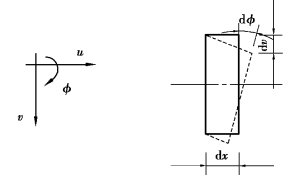
图4.13 截面的弯曲变形、剪切变形
截面变形向量表示为:
![]()
有效截面力向量自然也包含两个分量,即截面剪力和截面弯矩。表示为截面力向量有:
![]()
在截面层面上,剪、弯变形相互独立,容易建立此时的截面刚度矩阵为:

2)位移、变形函数分布
引入剪切变形影响后,对应切向位移的挠曲线中,有一部分是截面剪切效应的贡献,将梁位移曲线拆分为两部分 (x)和
(x)和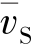 (x),即:
(x),即:
![]()
式中  (x)——弯曲变形对位移曲线的贡献;
(x)——弯曲变形对位移曲线的贡献;
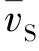 (x)——剪切变形对位移曲线的贡献。
(x)——剪切变形对位移曲线的贡献。
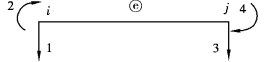
图4.14 结点自由度
本章单元分析是以截面分析为基础的,故本类单元仍直接推导考虑剪、弯效应下,截面的变形插值函数。根据截面变形插值函数的特点,在单元自由度下进行以下计算。(如图4.14所示,箭头指向为杆端自由度的约定正向)
(1)第1自由度
根据变形插值函数定义,在第1自由度发生单位位移时,截面变形分布包括独立的剪切变形和弯曲变形,推导如下(图4.15至图4.18中,内力图所标示符号为内力分布和对应变形分布在约定坐标下的正负):
梁i端向下发生单位位移,杆端剪力FQi(剪力分布沿杆长为常数,以剪力值常数绝对值FQ为参量),杆端弯矩Mi。根据图4.15(b)所示内力图和对应的刚度特征,建立位移方程:
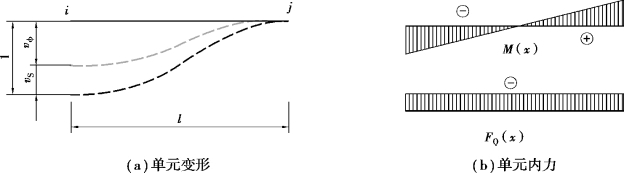
图4.15 第1自由度单位位移的变形与内力
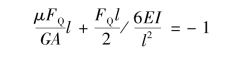
可解出:
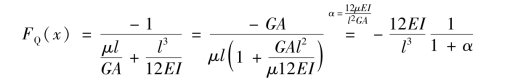
根据单元刚度矩阵元素定义,可知此剪力值的绝对值即为单元刚度矩阵元素k11,也可使用此方式计算出其余单元刚度矩阵元素。
由于剪力和剪切变形沿杆长均为常数,对应于第1自由度的截面剪切变形分布函数Bv1(x)可表达为:

根据剪力函数,截面弯矩(约定上部受拉为正)沿杆长分布函数为:
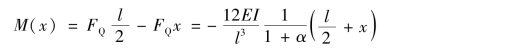
对应于第1自由度的截面变形分布函数Bϕ1(x)可表达为:

(2)第2自由度
对应于第2自由度,引入剪切变形。由于剪力FQ存在,杆端亦应由于剪切变形而产生vs的相对切向位移。故需要在此状态上表达出如图4.17的受力模式,保证单元对应于第2自由度发生单位转角位移,而i端切向位移仍需维持为0。
剪切变形对应的切向位移可表达为:(https://www.daowen.com)

以上切向位移和i端单位转角下,ij两截面弯矩值分别为:

由约束方程Mi-Mj=FQl,可解得:
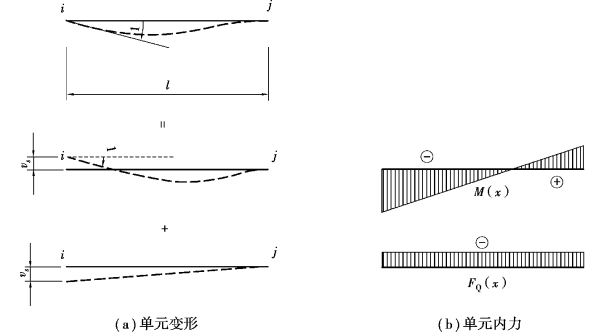
图4.16 第2自由度单位位移的变形与内力
![]()
即可知截面剪切变形分布函数为:
![]()
截面弯矩分布函数为:
![]()
弯曲变形分布函数Bϕ2(x)可表达为:
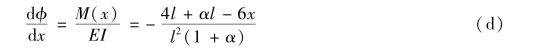
(3)第3自由度
第3自由度下的推导过程与第1自由度类似,如图4.17所示。
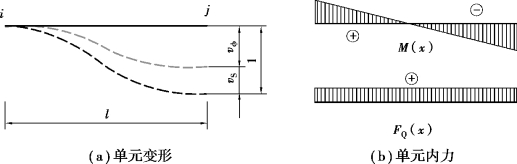
图4.17 第3自由度单位位移的变形与内力
可得:
![]()
弯曲变形分布函数Bϕ3(x)可表达为:

(4)第4自由度
第4自由度下的推导过程与第2自由度类似,如图4.18所示。
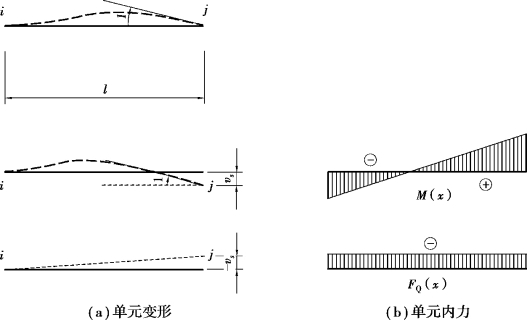
图4.18 第4自由度单位位移的变形与内力
可得:

据式(a)—式(i),合并以上各系数,即可得考虑剪切变形时的变形插值函数矩阵为:
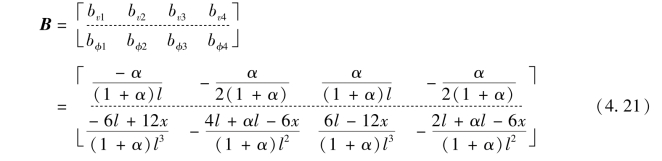
代入式(3.14),即有:
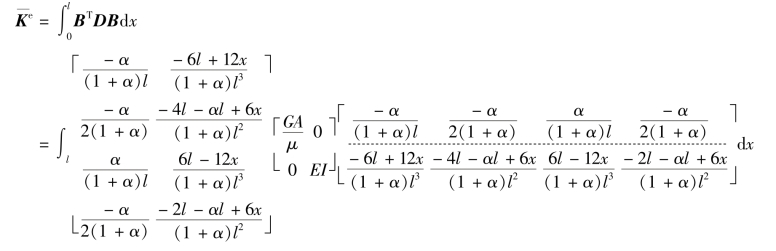

式(4.22)即为考虑剪、弯变形时平面杆元的单元刚度矩阵。
【说明】
将式(4.22)与未考虑剪切变形时单元刚度矩阵元素[式(4.18)]比较,参数α=12μEI/l2GA反映了杆件剪切变形的影响程度,主要因素包括截面的弯、剪刚度比和杆长。当杆长较长而截面弯剪刚度比值较小时,α较小,剪切变形的影响可忽略不计。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







