将各矩阵表达式代入式（3.14b），对于等截面桁杆，因B、D均为常数，可得：

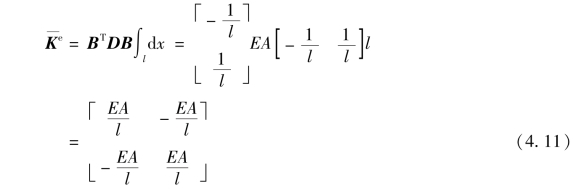
式（4.11）即为等截面桁杆的单元刚度矩阵。

【例4.1】某桁架中杆件为均匀变截面杆，截面参数如图4.8所示。若假定截面位移沿杆长为线性分布，试完成此单元的单元分析。

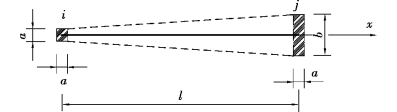
图4.8　变截面桁杆单元分析

【解】（1）截面的位移插值函数仍可写为：

（2）截面的变形矩阵B仍写为：

（3）截面弹性矩阵D形式也不变，但截面面积A应表示为变量x的函数，即：

（4）据式（3.14b），有：

(www.daowen.com)

式中，除截面面积A（x）为变量外，其余数值均为常数。

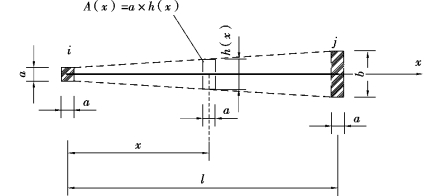
图4.9　截面的面积函数A（x）

如图4.9所示，将截面面积表达成位置x的函数，即得：

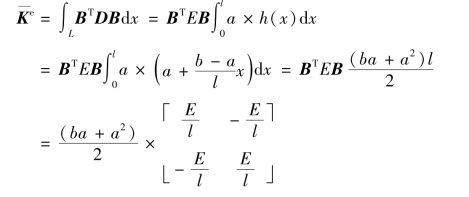
【说明】

（ba+a2）/2为单元截面面积沿杆长的平均值。根据积分计算过程，可知：

（1）对于均匀变截面桁杆，若设定位移分布沿单元轴线为线性分布，则其单元刚度元素与等截面杆单元刚度矩阵元素类似，只需以“平均截面面积”替换原等截面杆截面面积。

（2）显然，对于非均匀截面杆件，两结点桁杆单元的位移设定仍为线性分布，而变形为常数：

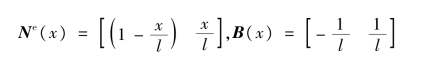
由于截面为变刚度，所以即使截面轴力为常数，真实变形沿杆长的表达式FN/EA（x）也并非如上式中B（x）一般为常数，分析结果是以积分段“平均变形”去替代真实变形分布。

【例4.1】所示单元，截面面积沿杆长线性变化，常轴力下杆件截面的真实变形也为线性分布，“平均变形”可有效表示杆长范围内的变形关系，在结点自由度层面也可准确反映结构的整体刚度关系。

（3）工程分析时，特别是截面特征呈明显非线性时（如E非常量，而是内力的函数），平均化替代必然会产生相应的误差。因此，若对计算精度有更高的要求，可继续细化单元，以令积分杆段内位移、变形的分布与设定函数更接近，取得更优解答。