平截面假定适用时，结合小变形假定，截面（截面力、截面变形）在轴线处的响应可完整代表截面上其余点的响应。此时的杆件退化为一维单元，利用截面位移可计算出截面上任一点处的应变大小，利用截面力也可计算出截面上任一点处的应力大小。

根据杆元截面变形特征，杆件的单元分析可建立在截面分析的基础上。

1）截面轴向分析

对应于截面轴向受力，截面变形和截面内力在截面上为均匀分布，如图4.2所示。

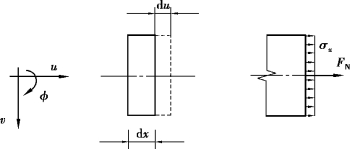
图4.2　截面轴向受力分析

可得轴向受力杆件的dx微段上轴向变形du（x）与轴力FN（x）的关系为

2）截面受弯分析

对应于截面弯矩，杆件微段存在弯曲变形，如图4.3所示。

图4.3　截面弯曲受力分析

根据平截面假定，可得微段dx上截面弯曲变形dϕ，与弯曲正应变εx沿截面高度分布的关系如下：

再由截面弯曲正应力与截面弯矩关系：

整理可得截面弯矩与微段弯曲变形之间的关系为：

3）截面剪切分析

实际的剪应力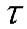（）、剪应变（γ）沿截面高度的分布必然是不均匀的，其分布函数取决于截面形状。截面分析时，可用“平均”剪应力和“平均”剪应变进行近似计算，此时截面的几何关系如图4.4所示。

图4.4　截面切向受力分析(www.daowen.com)

dx微段上，截面切向变形dv与截面“均匀化”分布剪应变γ之间的几何关系为：

截面剪应力（平均）的大小为：

式中　G——材料的剪切模量。

截面切向合力即可表达为截面剪力FQ：

式中　μ——剪应力不均匀系数，与截面形状相关。

矩形截面：μ=1.2；圆形截面：μ=10/9；

薄壁圆环截面：μ=2；工形截面：μ=全截面面积/腹板截面积。

可得微段上切向变形与截面剪力之间的关系为：

4）截面扭转分析

空间杆件还需要考虑杆件的扭转受力分析。若微段的扭转位移角用φ表示，截面抗扭刚度为GIx，微段上的扭转变形也可使用扭矩Mx和截面扭转刚度来描述，即

【说明】根据式（4.1）—（4.4），截面力向量FS（x）与截面变形向量fS（x）之间的变换关系（上标S表示此物理量对应于截面），利用截面刚度矩阵DS（x）表示，即截面刚度矩阵表达了截面变形与截面力之间的变换关系：

图4.5　截面扭转分析

满足平截面假定下，截面各变形分量相互独立。对需要同时考虑轴、剪、弯、扭等截面变形时，空间杆元的截面刚度矩阵可根据截面刚度关系进行列写：

对于不同受力特征的杆件，截面变形分量对杆件单元分析的影响程度不一。如桁杆可只考虑轴向变形的影响，梁式杆一般只考虑弯曲变形的影响，而平面杆和空间杆项次也有所区别。具体计算时，可根据截面变形的影响程度按需选择。