由图3.7及式(3.8)可知,位移插值函数即为结点位移(广义坐标)表达下的单元位移分布。
1)插值函数收敛性要求
有限元法的收敛性是指当划分的单元尺寸越来越小时,有限元法的解应该收敛于结构的精确解。基于位移法的有限元法求解过程,依赖于单元位移函数的选取。为了保证求解的收敛性,选取的单元位移函数应当满足下列两个条件。
(1)位移函数必须包含反映刚体位移的常数项和常应变的线性位移项。
单元的变形一般包括以下两个部分:
①因其他单元变形引起的单元整体的刚体变形。位移函数中显然必须包括常数项。
②自身变形引起的弹性变形。当单元的尺寸足够小时,单元内的应变比较均匀,近于常量。位移函数也必须要反映这一情况,才能保证收敛性得到满足。
(2)位移函数在单元内部必须连续,在相邻单元的公共结点上协调。
连续的结构体在受力后,其变形也是连续的(不能有断裂、重叠等现象),故描述单元内部响应的物理量也必须保持连续性。同时,还应尽量满足相邻单元间在边界处的协调。
2)位移插值函数计算
【例3.1】试推导两结点平面梁单元的位移插值函数。
【解】(1)如图3.8所示,梁单元不计轴向变形,杆端自由度为2,单元自由度为4。
根据收敛性的要求,位移插值函数必须包括常数项和线性项,选取三次多项式函数如下式:(https://www.daowen.com)
![]()

图3.8 平面梁单元位移插值函数
(2)式中包含4个待定系数(所选择的广义坐标,数目同单元自由度),可根据杆元始末端位移(即单元的边界条件)确定:

整理为:

(3)将待定系数代回位移函数,将位移表示为对应于广义坐标(即单元结点位移)的函数:

利用矩阵变换表达,即有:
![]()
(4)其中,变换矩阵即位移插值函数可写为:
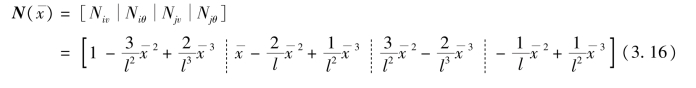
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






