根据位移法和矩阵位移法的原理，单元分析的目的是获取单元结点位移与结点力（对杆元，通常称为杆端）之间的变换关系，即寻找结点位移向量δe和结点力向量Fe之间的变换矩阵Ke，以建立单元的刚度方程：

结点位移向量δe是位移法分析的基本未知量，其分量取决于单元有多少结点、结点有多少自由度，与单元的受力与变形特征相关。

单元内部任一点（x，y，z）位移，都可以用位移分布函数u（x，y，z）表示。由于单元内部始终存在无穷多个连续点，故满足边界条件和连续条件的可能位移分布函数，原则上为无限自由度。按前所述，若单元已经足够细化，单元内部位移分布相对均匀，此时可尝试以确定性的简单函数去描述其内部位移分布。

根据位移法的概念，设定以单元的结点位移为描述位移分布的广义坐标，以此广义坐标去表达单元内部位移分布，截面位移分布函数便将随着每一个结点位移分量（广义坐标）的变化而变化。将位移分布函数利用里兹法的概念表达，可将无限自由度的单元内部位移分布函数简化为有限自由度体系，如图3.7所示。

为便于将函数映射用矩阵映射表示，将位移函数整理为插值函数的形式，即设定单元位移分布函数u（x，y，z）与结点位移δe之间存在着的变换关系为N（x，y，z）。出于公式表达上的简洁性和普适性的需要，在后续的分析中尽量省略变换关系中的坐标变量[如矩阵N（x，y，z）简写为N]，便可利用矩阵变换表达为：

单元内部存在着的应变分布亦为某函数ε（x，y，z），位移和应变的关系可利用弹性力学中的几何方程进行表达，即可认为存在此线性变换：

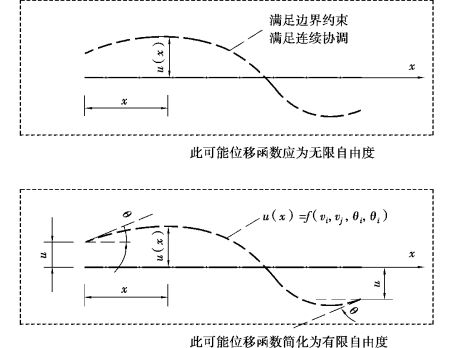
图3.7　广义坐标下的位移函数

令LN=B，L为微分算子，则有：

矩阵B一般称为几何变换矩阵或应变矩阵，可以将结点位移量变换成为单元内部的应变分布；而应力与应变之间应满足材料的物理方程，相应的变换可用弹性矩阵D来表达：

故有结点位移与应力分布之间的变换关系：

(www.daowen.com)

按弹性体虚位移原理，在单元弹性体发生任意可能的微小虚位移时（δ∗e、ε∗），真实外力（对单元，即此时的结点力向量）所做虚功，应等于单元体内部产生的虚应变能，即：

根据式（3.10）和式（3.12），将虚应变和应力分布的表达代入上式，即可得：

由于虚位移为“可能”位移，满足边界条件和连续、协调条件下可以任意发生，式（a）自然对任意虚位移也应成立，可从上式左右同时消去虚位移δ∗eT，得：

结点位移向量δe与单元内部积分无关，上式可以整理为：

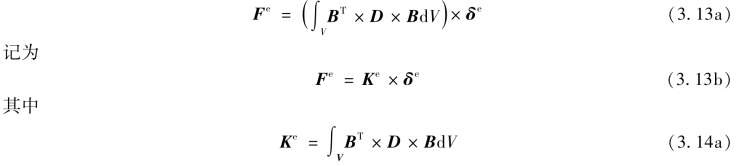
式中　Ke——单元结点位移向量与结点力向量之间的变换矩阵。

对于一维杆元，单元建立在截面分析基础上时，式（3.14a）可表达为：

式中　DS——截面力与截面变形之间的变换关系，即截面刚度矩阵；

　　　B——结点位移与截面变形之间的变换关系，即几何变换矩阵。

【说明】

据以上分析可知，结构单元状态的确定，可据不同线性空间中的物理量进行表达，如结点位移向量、位移分布函数、应变（截面变形）分布函数、应力（截面力）分布函数、结点力向量等。

单元分析时，可根据平衡方程、协调方程和物理方程，以及几何坐标变换，在各状态的对应向量间建立起相应的矩阵映射；而静力分析时，所有的变换关系整合后最终可反映至单元刚度方程（式3.13）中。

对于不同受力特征、截面特征、材料特征的单元，根据结构分析的需要（如计算量简化、精度要求、分析模式等），相应的变换关系可用精确或简化的矩阵映射进行表达。