下面先简单介绍里兹法，并以之引出有限单元法的基本思路。

1）里兹（Ritz）法

里兹法通过选择线性无关函数序列（里兹基函数）的线性组合，即利用里兹基函数构造的广义坐标系统，重新定义与原函数近似的响应函数：

式中　φi（x）——里兹基函数；

　　　αi——待定系数，即广义坐标。

如在使用瑞利（Rayleigh）法计算悬臂梁自振频率时，若所取振型曲线为结构的真实振型曲线，则可得真实解。但显然，结构的真实振型曲线y（x）未知，无从获取。而任意假设振型曲线的方式，让瑞利法计算结果的精度很难保证，此时便可利用瑞利-里兹法进行计算。

取广义自由度n=2，根据悬臂梁边界条件，选择里兹基函数

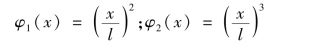
则有：

在基函数φi（x）选定后，y•（x）是以广义坐标（a，b）为变量的两自由度体系去拟合原无限自由度体系的y（x）。

还可调整自由度的数目，如取n=3：

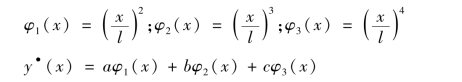
随着自由度n的增加，拟合效果通常会更好，对计算误差有较好改进作用，拟合接近程度决定计算的精确程度。

2）有限单元法(www.daowen.com)

里兹法是以全域分析的模式出现的，对于单杆体系外的工程结构，定义全域函数将非常困难，若将里兹法原理应用于子域（单元），便为有限单元法。

下面以截面位移分布的响应为例进行说明。在荷载或其他因素作用下，结构的每一截面均可能产生位移，而位移分布一定是某些变量的函数。即，位移分布始终可以表达为结构参数的某一函数，只是该函数的具体解析、表达和直接计算可能相对困难。

此时使用有限单元法（基于位移场）的基本思维模式为：结构的位移分布函数是复杂的，但可以设想，在一较小杆段区域范围内，位移的分布会相对均匀；并随着杆段减小，区域长度越小，位移分布的均匀程度或许越好。最极端的情况是：当区域缩小到为一个点（对杆而言，即为截面）时，位移分布自然就是完全均匀的，如图3.6所示。

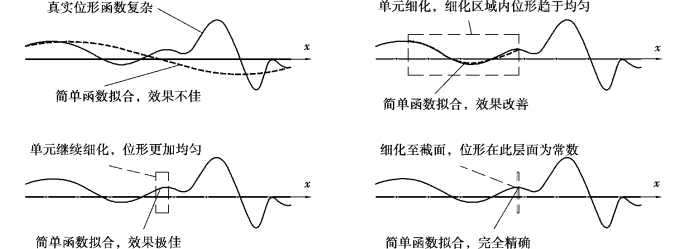
图3.6　单元细化程度与位形函数拟合

在线弹性杆系结构静力分析时，一般并不需要过多地考虑响应函数究竟在多长杆段范围内才会“足够”均匀。其原因是在常规受力模式下，自然杆段离散后所对应的杆件内，单元的实际位形函数并不会过于复杂。

下面以平面梁（等截面直杆）静力分析为例进行说明。结点力作用下时，由杆件的平衡条件可知，截面弯矩沿杆长分布为线性，截面弯曲变形正比于截面弯矩，分布也应为线性：

按材料力学知识可知截面位移分布函数为：

因此，对于一个杆件单元，若使用三次多项式对位移分布函数进行拟合，在接受简化（如平截面、小变形、线弹性等假定）所带来的误差后，位移分布函数就是精确的。

综上，说明在直杆单元中，用简单函数拟合所表达响应函数较为有效。当然，杆元的静力分析是一个特例，若在动力分析、稳定分析、非线性分析中用简单函数去描述直杆的可能位移分布，很难在自然杆段的单元划分原则下就取得较好的效果（参见第6章动力分析相关内容）。但可以接受的是：以简单函数去模拟真实的函数分布，随着单元细化，误差总会趋于减小。

由此，可得有限单元法分析时的基本思路为：

①将结构离散、细化为若干单元。

②细化后的单元内部响应（位移、应力、应变或其他）会趋于相对均匀。

③利用设定的简单函数近似模拟单元内部响应分布（在单元内应用里兹法）。