1）弹性体虚位移原理

虚功原理中，仅外荷载和位移边界条件是确定量，内力分布只是满足平衡条件下的“可能”内力；位移与变形皆是“可能”位移与“可能”变形；可能的变形状态，与外力和“可能”内力之间，不存在方程约束，可以完全无关。

现若让内力对应于真解，即结构处于真实的唯一平衡受力模式中[注意式3.1（c）中，各力项的上标不再有“∗”]，只让微小的位移、变形在可能范围内，自行满足对应的约束方程取得协调。此时的“可能”位移与变形，与结构真实受力模式无关，只表达满足约束方程的一切“可能”位形，称为虚位移。根据以上条件改写式3.1（a），有：

即可由虚功原理直接表达出虚位移原理：弹性体处于平衡状态的充分必要条件是，对于任意微小虚位移，作用在弹性体上的外力所做虚功，应等于弹性体内的虚应变能。

虚位移原理使用的是结构的真实平衡状态，故虚位移原理与静力平衡方程等价。

2）杆系结构的虚功表达

以上公式推导过程以仅受轴力的桁杆为例。本书分析对象为一般杆元，如图3.4所示。根据截面受力和变形特征，可将上述公式推广至一般的杆件单元中。(www.daowen.com)

在一般杆系结构中，做功的外力包括荷载和约束力。按分布力和集中力区分，外力虚功可表达为：

当杆系分析建立在截面上时，内力由截面力分量表示（截面弯矩、剪力、轴力），而变形则由截面变形分量表示（截面弯曲、剪切、轴向变形）。平面杆系结构中虚应变能可写为：

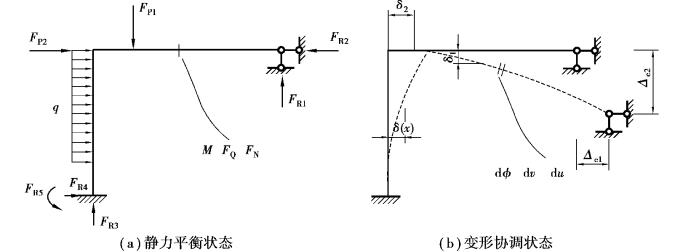
图3.4　一般杆系的虚功表达

式（3.6）适用于平面杆系中同时考虑轴向、剪切和弯曲变形的杆件，可用于表达虚功原理和虚位移原理中应变能的计算式。若对象为空间杆件，也可根据截面力和截面变形的分量构成进行扩展。