1）弹性体虚功原理的证明

以下推导中，上标“∗”表示该物理量为“可能状态”，即：力满足平衡条件，变形满足连续协调条件；但并不一定对应于结构的真实响应。同时，变形应是微小的，以保证结构变形时，力的位置和方向改变量均可忽略，平衡模式不变，力可与原作用位置处对应位移相乘做功。

下面以图3.3所示桁架杆单元为例进行介绍。

如图3.3（a）所示，外荷载确定时，单元的可能内力分布为也存在无穷多组满足平衡条件下的可能状态，但任一的可能状态，必满足以下平衡方程，如图3.3（b）所示。

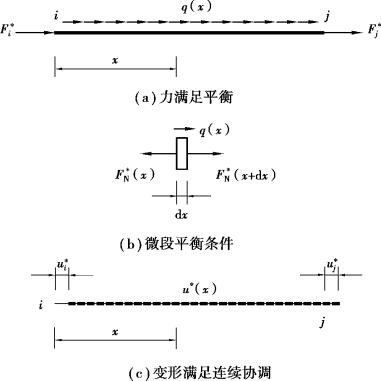
图3.3　桁杆单元的虚功原理

将平衡条件式（a）乘以“可能”位移分布u∗（x）（即让微段dx上的平衡外力在微段位移上做功），并沿杆全长积分。由于受力过程中平衡条件始终成立，积分结果为0，故有

将上式展开，写为

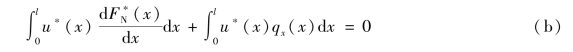
对式（b）第一项分部积分，有

注意到“可能”位移状态中[如图3.3（c）所示]，有：(www.daowen.com)

式（d）保证了桁杆单元中，位移与变形之间的连续协调。将式（d）代入式（c），整理并移项，可得：

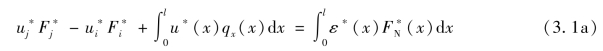
式3.1（a）等号左侧，和qx（x）分别为“可能”杆端力和荷载，对单元而言，皆为外力，故外力在对应“可能”位移上做功：

式3.1（a）等号右侧，“可能”内力在“可能”变形上的应变能为：

式3.1（a）是根据桁杆单元建立的，对于梁杆单元或其他弹性单元体，根据内力和变形的不同形式，最后同样可表达为：

鉴于力与位移皆仅为“可能”状态，力与位移之间不要求存在状态关联，外力功即为虚功，而应变能也为虚应变能。

由此，可得到弹性体虚功原理的表述：

“可能”外力在“可能”位移上所做的虚功，应等于“可能”内力在“可能”变形上所引起的虚应变能。

2）虚功原理的说明

虚功原理的成立仅涉及平衡条件与变形连续协调条件，与材料性质无关，故其适用性强。