1）静力平衡条件

结构的静力平衡条件，是结构分析最常使用的约束方程。静力分析时，结构整体或任一局部，都应该满足静力平衡条件。

基于不同的受力模式，对研究对象（结构、单元、微段）在描述运动的坐标空间任一维度上，或是平动，或是转动，均应有：

对静定结构，该方程组可以确定体系的反力和内力分布。但若存在多余约束，由于未知量数目始终大于独立平衡方程数，因此必然存在无穷多组同时满足平衡方程的解。

如图3.1（a）所示的超静定结构，在图3.1（b）中的两组不同平衡状态下都满足平衡条件。

因此，满足平衡条件的解，只能称其为“可能”解，并不一定是结构的真实解。

2）变形协调条件

除平衡条件外，结构受力时另一状态便是变形状态。结构受力过程中，变形应该保持连续、协调，并保证与边界约束一致。变形状态也有对应的约束条件，满足设定约束条件的变形，即为“可能”变形。“可能”变形同样有无限多种状态。如图3.2（a）所示结构，图3.2（b）所给出的两种变形状态都为变形协调条件允许。(www.daowen.com)

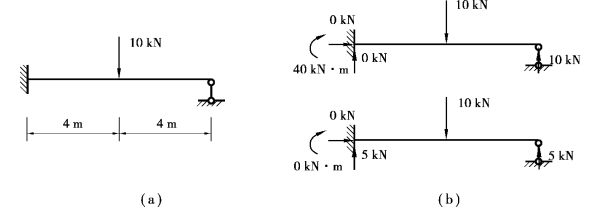
图3.1　“可能”的平衡条件

同样不能仅依据变形协调条件，确定结构的真实状态。

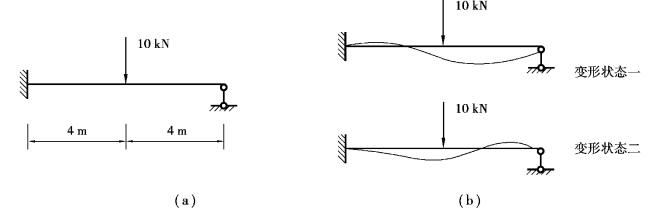
图3.2　“可能”的变形条件

显然，以上两个条件同时成立，才能对应于结构受力时的代数解。

【说明】

上文中没有提到代数解的唯一性，事实上，同时满足平衡方程和位移协调的代数解也可能存在多组甚至无穷多组。本书研究范围限定在线弹性小变形的范围内，且平衡条件不变，即默认代数解唯一，就对应于真解，关于更多解的可能性在此不再深入讨论。对结构状态和真实解性质有进一步认识需求的读者，可去了解最小势能原理和势能驻值原理。