利用单元定位向量所集成的结构刚度矩阵K和综合结点荷载向量F，建立结构刚度方程如下：

用先处理法形成的结构刚度方程是线性代数方程组，其系数矩阵对称正定，可用线性方程高斯消去法求解，也可使用逆矩阵进行求解。

求解此方程组，即可得到未知结点位移Δ的唯一确定解。

后续计算步骤包括：

①求解结构刚度方程，计算出结点位移向量Δ；

②根据各单元定位向量，获取各单元的杆端位移向量δe；

③根据杆端位移向量δe，计算出单元坐标系下对应此位移向量的单元杆端力向量

④与单元荷载作用下的单元固端力向量叠加。

【例2.4】试用先处理法计算例【2.2】中刚架[重绘于图2.18（a）]的内力。已知各杆EA=4.8×106kN，EI=0.9×105kN·m2。

图2.18　例2.2图

【解】（1）结点编号、单元编号、结构位移分量编码及结构坐标系、各单元坐标系如图2.18（b）所示。

（2）各单元定位向量为：

（3）根据结构坐标系中的刚度矩阵Ke元素定义，计算出各单元刚度元素，并将单元定位向量写在单元刚度矩阵的上方和右侧。

单元①：

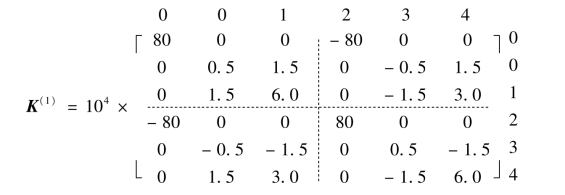
单元②：

单元③：

利用单元定位向量，“对号入座、同号相加”，形成结构刚度矩阵K：

(www.daowen.com)

结构的综合结点荷载列阵F已在【例2.2】中求得，为：

形成结构刚度方程KΔ=F，即：

解方程，得结点位移Δ为：

计算各单元杆端力，即：

单元①：α=0°，

单元②：α=0°，

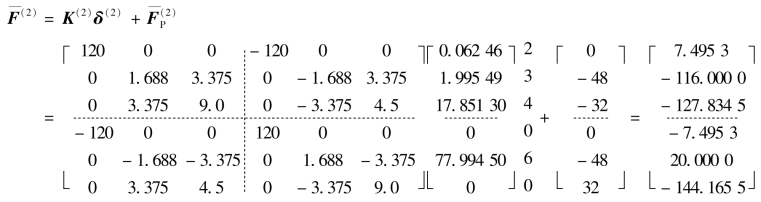
单元③：α=π/2，

根据上述计算结果作内力图，如图2.19所示。

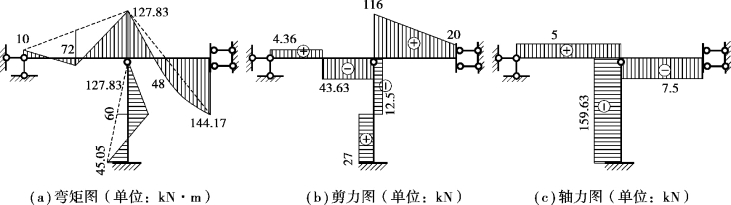
图2.19　内力图

【说明】

矩阵分析所得杆端力的正负，是根据单元坐标系中对应分量的约定方向所定；而绘内力图时仍应按结构力学中截面力正负约定进行表达。图2.20中表明了杆端力方向（矩阵分析）与截面力方向（结构力学）之间的关系。

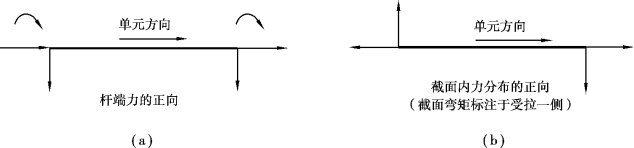
图2.20　杆端力与截面力正负关系

【程序实现】

杆端力计算根据式，仍以一句程序语句实现，其中数组D_NOD是以结构刚度方程解出的结点位移向量Δ。