1）结构刚度矩阵的集成

对结构坐标系下的单元刚度矩阵，利用单元自由度与结构自由度之间的对应关系（即单元定位向量），也可取得结构刚度矩阵。手算时的具体做法为：

①计算单元ⓔ在结构坐标系中的刚度矩阵Ke，分别注明其定位向量中各分量（始末两端结点未知量编码）及单元自身的结点位移分量编码（数字上加画一短横线表示为单元局部码）。

②按照单元定位向量中的非零分量所指定的行码和列码，将各单元刚度矩阵Ke中的元素“对号入座”地叠加到结构刚度矩阵K中去，行、列码相同的元素则相加。

【例2.3】试按单元定位向量装配如图2.17所示连续梁的结构刚度矩阵。

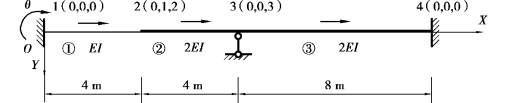
图2.17　按单元定位向量集成结构刚度矩阵

【解】（1）对连续梁进行结点编号、单元编号和结点未知量编码，如图2.17所示。

根据各单元始末两端的结点未知量编码，形成各单元的定位向量，即

（2）列出3个单元的结构坐标系中的刚度矩阵。

由于连续梁的单元坐标系与结构坐标系是一致的，故无须坐标变换。所列出的K（1）、K（2）、K（3）如下式（a）、（b）、（c）所示。将总码和局部码分别写在各单元刚度矩阵的上方和右侧，便于对位相加。

按照单元定位向量中的非零分量（即总码中的非零编码）所指定的行码和列码，将各单元刚度矩阵Ke中的元素定位叠加到结构刚度矩阵K中去。

以单元①为例：

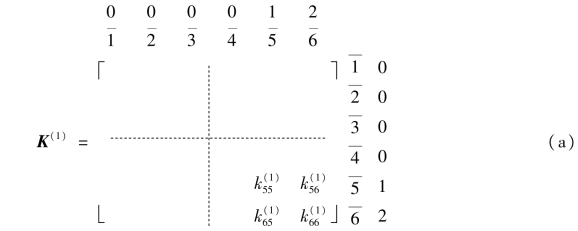
由式（a）可知，总码中的非零编码仅为1和2，对应着局部码。因此，按它们指定的行号和列号取出的单元刚度系数只有4个（元素的上标为单元号，下标为单元码中的行、列号），如式（a）所示。

同样，也可将单元②和单元③中非零编码所对应行、列中的相关单元刚度系数逐一取出，按照“对号入座，同号相加”原则，送入并叠加到结构刚度矩阵K中去。

最后形成的结构刚度矩阵如下：

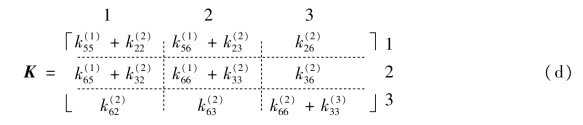
2）结构刚度矩阵的特性

根据结构刚度矩阵集成过程，可将单元定位向量中拥有结点位移编码i的所有单元，都称为对应于未知量δi的相关单元；将与未知量δi属于同一个单元的其他未知量，称为δi的相关未知量。

结构刚度矩阵有如下一些特性和组成规律：

①结构刚度矩阵K是（N×N）阶方阵，N为结点位移未知量数。

②结构刚度矩阵K为对称矩阵。

其对称性可由线弹性结构的反力互等定理证明。K中对称于主对角线的元素两两相等，即kij=kji。(www.daowen.com)

③结构刚度矩阵K为正定矩阵。

在结构受力过程中，根据能量守恒，外力做功W应转化为变形体内的应变能U。而结构发生任意结点位移Δ时，静力荷载做功可表达为：

在稳定结构中，对应于任意结点位移发生时的变形状态，结构存贮的应变能U恒正。因此，以下变换恒成立：

故结构刚度矩阵K为正定矩阵，可逆。

④结构刚度矩阵元素与单元刚度元素有关系。

a.主对角元素kii由未知量δi的相关单元刚度矩阵的相应主对角元素叠加而成。

如【例2.3】中，由式（d）有：

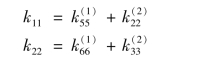
b.非对角元素kij有两种情况：

若未知量δi与δj是相关未知量，则kij=kji≠0。

若未知量δi与δj不是相关未知量，则kij=kji=0。

⑤大型结构刚度矩阵一般是稀疏矩阵。

结构规模越大，总未知量中可通过单元联系的相关未知量所占比例就越小，有意义的非零元素数目就越少，故大型结构刚度矩阵一般是稀疏矩阵。

⑥大型结构刚度矩阵K为带状矩阵。

非零元素一般分布在主对角线的附近，矩阵元素分布将表现出明显的带状特点。

注意：矩阵正定、稀疏、带状分布的特性，对矩阵数据存储和计算方法中的优化意义重大。本书主要立足于基础力学概念认识，分析时仍使用满阵存储和直接求解，对存储及计算的优化未作涉及，有兴趣的读者可参阅其他相关资料。

【程序实现】

（1）单元刚度矩阵通过坐标变换至结构整体坐标系统下。

（2）按自由度对应关系传送进入结构刚度矩阵。

【例2.3】中采用的人工定位进行传送，操作复杂。程序实现时可利用传送矩阵，处理则可非常简洁。

利用单元定位向量构造的传送矩阵Se，将单元刚度矩阵元素传送至结构刚度矩阵内。

坐标变换和式（2.19）的变换，通过以下程序语句实现：