当结构上的某些荷载作用在杆件单元上，而非直接作用于结点时，称为单元（或非结点）荷载。必须先将单元荷载转换成等效结点荷载（等效原则是要求两类荷载作用下，结构的结点位移应相等），然后才能用矩阵位移法进行结构分析。

1）计算在单元坐标系中的单元固端约束力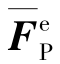

如图2.15（a）所示的刚架，在单元②两端各加上3个附加约束，使其两端杆端位移为0，可求出6个固端约束力，如图2.15（b）所示。按单元自由度约定方式排列，即组成单元②的固端约束力向量。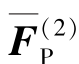

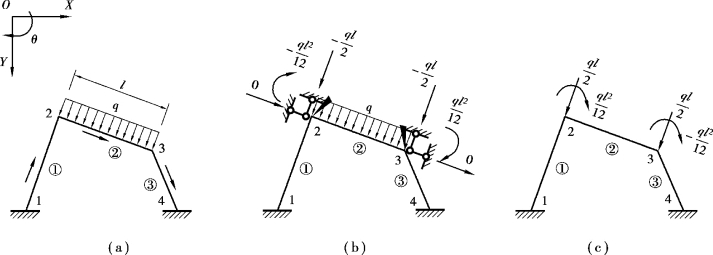
图2.15　单元等效结点荷载

表2.1中给出了一些典型荷载作用作用下单元的固端约束力。固端约束力分量的正负号规定，仍遵从单元坐标系统约定。

表2.1　单元坐标系下固端约束力

续表

2）单元坐标系中的单元等效结点荷载

由于杆端力与结点力为相反力，将固端约束力反号，可得到单元坐标系中的单元等效结点荷载，即

对于图2.15所示单元②，有

3）结构坐标系中的单元等效结点荷载

将进行坐标变换，得到结构坐标系中的单元等效结点荷载，即

根据单元自由度与结构自由度的对应关系（即利用单元定位向量），可将每个中的元素，传送到结构的等效结点荷载列阵FPE的相应位置。所有单元的等效结点荷载列阵在对应自由度位置进行叠加，便可得到结构等效结点荷载向量。

4）综合结点荷载向量

将直接结点荷载向量FJ与等效结点荷载向量FPE进行叠加，即得到综合结点荷载向量。

【例2.2】试求图2.16（a）所示结构的综合结点荷载向量F。

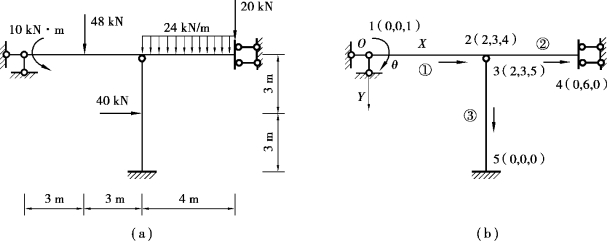
图2.16　计算综合结点荷载向量

【解】（1）结点编号、单元编号、结点未知量编码及单元、结构坐标系统如图2.16（b）所示。

（2）计算单元固端约束力。

按表2.1所列计算式，可求得：

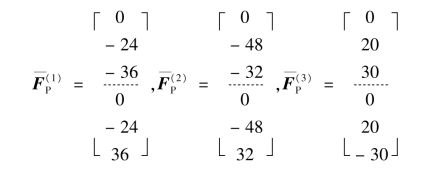(www.daowen.com)

（3）计算单元等效结点荷载，并将单元定位向量写在的右侧，以便于定位传送，即有

单元①：

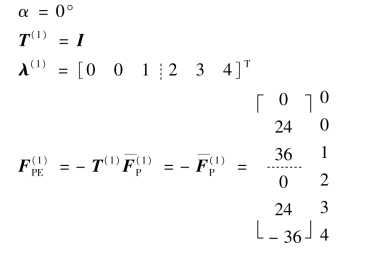
单元②：

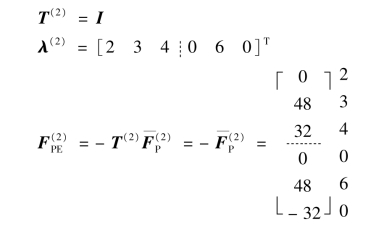
单元③：

（4）利用单元定位向量形成等效结点荷载列阵FPE。

按单元定位向量，根据自由度对应关系“对号入座”，可得等效结点荷载列阵为：

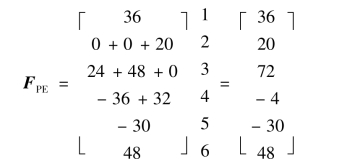
（5）形成综合结点荷载列阵F。

通过以上计算，将非结点荷载转化为结构的等效结点荷载FPE，再与直接结点荷载FJ叠加，即得：

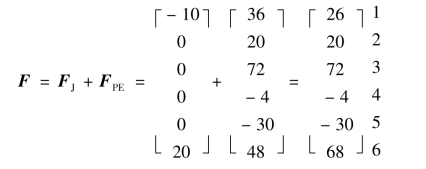
【程序实现】

（1）按表2.1，形成各类单元荷载对应的单元坐标系下单元等效结点荷载向量。

MDA程序中通过子程序EFF（）实现。

（2）变换至结构整体坐标系，即式（2.14）。

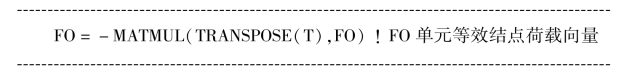
（3）利用自由度对应传送的原理，通过矩阵变换的方式传送入综合结点荷载向量。

构造传送矩阵S（N×m），行数N为结构总自由度数目，列数m为单元自由度数目（对平面一般杆元，m=6）。由于单元定位向量反映了单元自由度与结构总自由度的对应关系，可根据元素在向量空间定位传送关系[式（1.2）]，故有：

S矩阵中共有m=6个列向量S1~Sm，每一列向量Si中最多只有一个非零元素，即

以下为构造平面杆元数据传送矩阵对应程序语句：

可利用变换式（2.16），将单元等效荷载向量中的数据，按自由度对应的关系，从单元分析自由度传送至整体分析自由度下。

式（2.18）也只需要一句程序语句即可实现：