杆端位移影响单元变形和内力。由于结点的约束效应，一般情况下，杆端位移可根据结点位移进行表达，故结点位移成为体系计算的基本未知量。而结点位移编码，就是对体系所有可能产生的结点位移，按结构整体坐标系中的分量约定，连续编码，以确定结点位移向量的基本构成。

平面杆系结构的每个结点（此处所指为刚结点、无外约束）在整体坐标系下有3个位移分量（u，v，θ）。采用先处理法计算时，应按照结构的结点顺序，依次对每个结点的未知位移分量u，v，θ统一编码（即结点位移编码，也称为结点未知量编码）。

为便于程序编制，有几个约定，说明如下：

①对于取作基本未知量的结点未知量，连续编码，即1，2，…，n。

例如，图2.10中的刚结点1、2、3，各有3个结点未知量，故它们的结点位移编码分别为（列写于结点编号后括号内）：

结点1（1，2，3），结点2（4，5，6），结点3（7，8，9）。

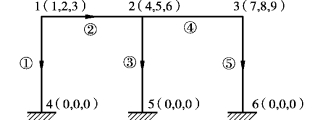
图2.10　结构位移分量编码

②对于已知的支座结点位移分量（包括为零和非零），编“0”号。

由于外约束对应的结点位移分量为已知值，不属基本未知量，应加以排除。例如，图2.10中的固端支座处结点4、结点5、结点6，在X、Y、θ3个方向都不可能产生未知位移，故它们的结点位移编码均为（0，0，0）。

先处理法中，对于支座处存在非零位移值者，对应位移分量仍应编“0”号，而将支座位移以单元广义荷载的形式引入。(www.daowen.com)

③当平面刚架内部有铰结点（全铰或半铰结点）时，由于铰结点无法协调连接各杆端的转角位移，结点转角将无法表达所有的杆端转角分量，为继续遵从“以结点位移表达杆端位移”这一约定，需要使用“重结点”编号模式。即对无法用单结点位移表达所有杆端位移处，增设一个（或多个）单独的结点号。

如图2.11（a）中，结点A连接的单元①、单元②的两个杆端，杆端位移分量中线位移相同，而转角不同，故结点对应的杆端位移不完全相同；它们的线位移分量采用相同编码，而转角采用不同编码，此时结点未知量编码分别为：结点2（1，2，3）、结点3（1，2，4）。图2.11（a）中结点B的情况也是如此。

上述方式也可用于处理定向结点，如图2.11（b）所示的结点C。由于结点C无法协调其左、右两侧竖向位移，所以引入重结点编号，保证两重结点间竖向位移相互独立。

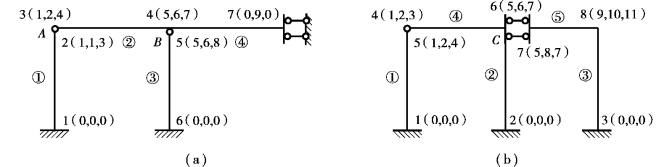
图2.11　内部有特殊结点时的结点位移分量编码

④对于无效结点未知量（即计算中不需考虑的结点未知量），编“0”号。例如，平面桁架中的结点[如图2.12（a）中结点1、2、3、4]或平面组合结构中桁杆之间的铰结点[如图2.12（b）中结点7、8]，由于桁杆转角与弹性变形（即内力）无关，杆端转角位移分量不需要考虑，故编“0”号。至于连接一般单元与桁架单元之间的铰结点[如图2.12（b）中的结点1、2、5、6]，因其杆端转角位移分量仅仅影响与其连接的一般单元，而不影响与其连接的桁架单元（后者EI=0），故这些结点仍具有3个独立的位移未知量（分别为0，0，1；2，3，4；9，10，11和12，0，13），不需进行处理。

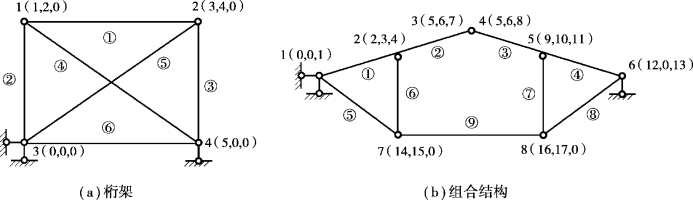
图2.12　有无效未知量的结点位移分量编码

对于忽略轴向变形的刚架，刚结点在某些方向上的位移分量不一定独立。如图2.13所示刚架，当忽略各杆的轴向变形时，横梁上结点2、3、4的水平位移X2=X3=X4，它们是同一个未知量，因此采用相同的结点未知量编码“2”。同理，柱（单元①）两端结点1、2的竖向位移Y1=Y2=0，因此采用相同编码“0”；柱（单元③）两端结点5、3的竖向位移Y5=Y3=0，因此也采用相同编码“0”。

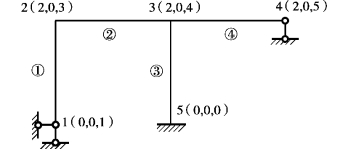
图2.13　忽略轴向变形时结点位移分量编码