1）截面力向量的坐标变换

平面杆系结构任一截面力向量，需要以3个分量描述其构成元素。此时存在两个坐标系统：单元坐标系统和结构坐标系统（X-Y-θ）。规定由X轴到x轴的夹角α以顺时针旋转为正，如图2.6所示。

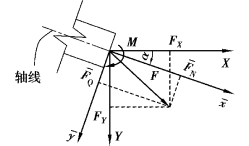
图2.6　截面力在不同坐标系统下的分量表示

由式（1.9），并结合考虑平面体系中坐标系旋转变换与转动自由度无关，故有

写成矩阵形式，为

即在不同直角坐标系之间，截面力向量使用坐标变换矩阵T0进行坐标变换。

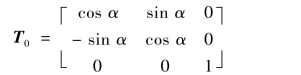
显然，T0仍为一个正交矩阵，此时存在的线性变换为：

或

2）杆端力向量的坐标变换

杆单元杆端力向量由杆件的始端杆端力和末端杆端力构成，共包含6个分量，如图2.7所示。

图2.7　单元坐标变换

始端杆端力和末端杆端力在坐标系之间，分别满足以上变换式（2.5）。因此，单元坐标系下的杆端力，结构坐标系下的杆端力Fe若分别表示为：

则根据式（2.5），应有以下坐标变换成立：

或展开写为

或简写成

式（2.6）中

称为一般平面杆单元的坐标转换矩阵。T仍为正交矩阵，因而有

3）杆端位移向量的坐标变换

杆端力向量的坐标变换方式，也同样适用于杆端位移向量之间的坐标变换，即

或

4）单元刚度矩阵的坐标变换(www.daowen.com)

将式（2.9）代入，有：

式（a）左右同时左乘TT，可得：

即结构坐标系下的杆端位移向量与杆端力向量之间的变换关系，由3个矩阵的乘积决定，式（b）可写为：

此即为结构坐标系中的单元刚度方程。其中

式中，Ke为结构坐标系中的单元刚度矩阵。

根据矩阵知识可知，为相似变换，实对称矩阵经此变换后仍应为对称性不变，矩阵特征值也不会改变。因此，结构坐标系统下的单元刚度矩阵Ke仍然是对称矩阵；Ke仍然是奇异矩阵。由于执行了坐标变换，Ke除与单元本身的属性有关外，还与结构坐标系与单元坐标系之间的夹角α有关。

Ke中任一元素表示结构坐标系下杆端位移δe中第m个分量等于1（其余位移分量均等于零）时，所引起的杆端力Fe的第l个分量的值。单元坐标系与结构坐标系间的关系较规整时（如α=0°或90°），也可按概念直接推导结构坐标系统下的单元刚度矩阵元素。

【例2.1】试以单元刚度系数的概念，直接写出如图2.8所示结构各单元在结构坐标系统下的单元刚度矩阵。各杆EI、EA为常数，结构坐标系和单元坐标系如图2.8所示。

图2.8　单元刚度矩阵元素

【解】（1）对于单元①：

α=90°，若按式（2.12）计算，执行矩阵乘法计算量较大，故根据单元刚度元素kij的性质进行元素推导，如图2.9所示。

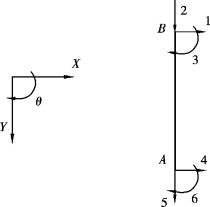
图2.9　结构整体坐标系下的杆端自由度

kij的意义为：在结构坐标系下，杆端自由度j发生单位位移，在i自由度方向上需作用力的大小。

令杆AB在沿1方向发生水平单位位移，确定对应杆端力，由形常数即有：

令杆AB在沿2方向发生竖向单位位移：

令杆AB在沿3方向发生单位转角：

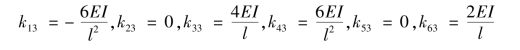
令杆AB在沿4方向发生水平单位位移：

令杆AB在沿5方向发生竖向单位位移：

令杆AB在沿6方向发生单位转角：

可得单元①的单元刚度矩阵为：

（2）对于单元②：显然，单元②的单元刚度矩阵与单元①的单元刚度矩阵相同，有：

（3）对于单元③：α=0°，单元刚度矩阵在两个坐标系统中是相同的，即式（2.4）的形式，此处不再列写。