平面杆系一般单元的单元刚度方程中，单元坐标系下杆端位移向量与杆端力向量之间的转换矩阵为：

式中，称为单元坐标系中平面杆系结构中一般杆单元的单元刚度矩阵，是6×6阶的方阵。

1）单元刚度矩阵元素的物理意义

单元刚度矩阵中元素称为单元刚度系数，代表由于单位杆端位移引起的杆端力。任一个元素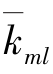，表示第l个杆端位移分量等于单位位移（其余位移分量等于零），所引起的第m个杆端力分量的值。例如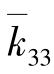，=4EI/l，表示第3个位移分量θi=1时，所引起的第3个杆端力分量Mi的值。

2）单元刚度矩阵是对称矩阵

单元刚度矩阵中位于主对角线两边处于对称位置上的两个元素相等，即

这一性质可由线弹性体系虚功互等定理得出。

3）一般单元的单元刚度矩阵是奇异矩阵(www.daowen.com)

式（2.4）中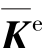的行列式之值等于零，不存在逆矩阵。

这表明，已知单元杆端位移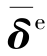，可唯一求出单元杆端力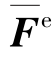，即

但若是已知单元杆端力，由于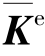（）-1不存在，故不能变换获取单元杆端位移。

从力学概念来看，这是由于形成单元刚度方程时，并没有考虑其他单元及结构支承对该单元的约束效应。无外界约束的一般单元，称为自由单元。自由单元在杆端力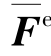作用下，除单元自身产生弹性变形外，还可以产生任意的刚体位移，故某一组满足平衡条件的杆端力可以与弹性位移和任意刚体位移组成的无穷多组杆端位移相对应。因此，已知杆端力并不可能取得唯一的杆端位移解。

4）单元刚度矩阵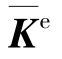是单元固有的性质

从单元刚度元素的构成看，其只与单元参数（E，I，A，l）有关，与外荷载和结构的其余部分皆无关。