1）两类坐标体系

矩阵分析时，需要将结点力、结点位移等物理量表达为向量，而向量空间的建立需要借助坐标系统。由于组成结构的各杆方向不尽相同，为了单元分析的方便，并进而与工程应用相适应，通常采用两类直角坐标系，在不同分析阶段对物理量分别进行描述。这两类坐标即为结构整体分析时的结构坐标系和单元分析时的单元坐标系，如图2.2所示。

图2.2　结构坐标系和单元坐标系

结构坐标系又称整体坐标系，用于参与结构整体分析的向量表达。平面体系分析时，结构坐标系常用用X-Y-θ表示，以X轴正向至Y轴正向的旋转方向为θ正向（对应于空间右手直角坐标系统）。由于工程结构中最常见的荷载为重力荷载，故惯常以竖直向下作为Y轴正向。

单元坐标系又称局部坐标系，用于参与单元分析的向量表达。平面体系分析时，单元坐标系用（或x-y-θ）表示，杆轴始端结点（i）指向末端结点（j）的方向（即轴向），约定为正方向；以x 轴的正方向顺时针旋转90°为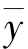轴的正方向。

2）单元坐标系中杆端力向量和杆端位移向量

单元杆端位置处的截面内力和截面位移，分别称为单元杆端力和杆端位移。如图2.3所示为平面刚架中的第ⓔ单元，其始端和末端的结点号分别为i和j。

单元坐标系x 轴沿杆单元轴向建立，单元坐标系统的3个坐标方向对应于杆件截面的轴向、切向和转动方向。平面杆单元的每个杆端截面有3个杆端力分量：轴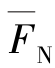力、剪力和弯矩M。与此相对应，单元的每个杆端截面也有3个杆端位移分量：轴向位移、切向位移v和角位移θ，如图2.3（a）所示。

单元分析时，杆端力和杆端位移分量均应按照约定的次序排列：先“始端”后“末端”，每端内力（位移）分量的排列次序是：。在单元坐标系中，单元的6个杆端力（位移）分量的排列序号如图2.3（b）所示。

(www.daowen.com)

图2.3　单元坐标系中单元的杆端力和杆端位移向量

单元坐标系中的单元杆端力向量和杆端位移向量可分别用表示：

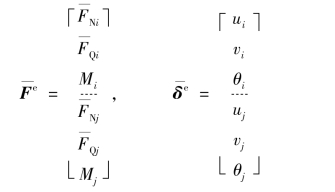
3）结构坐标系中的单元杆端力和杆端位移

在结构坐标系中，单元杆端力向量和杆端位移向量均应以结构坐标系统（X-Y-θ）进行分量表达，每个杆端截面仍有3个杆端力分量及相应的3个杆端位移分量，如图2.4（a）所示。单元两杆端共有6个分量序号的排列约定，如图2.4（b）所示。

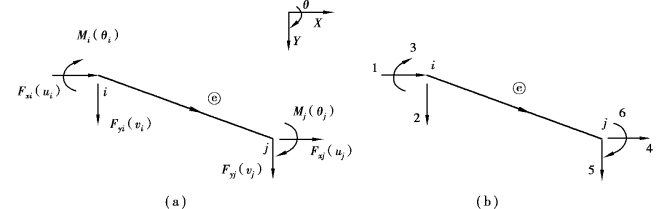
图2.4　结构坐标系中的单元杆端力和杆端位移

结构坐标系中的单元杆端力向量和杆端位移向量可分别用Fe和δe表示：

需注意，上述杆端力和杆端位移的正负号规定，均应按预设坐标系统下各分量的约定进行，与经典结构力学中位移法中规定并不完全相同。