进行坐标变换不会改变物理量的基本性质,只是描述物理量向量空间“基”的选择发生了改变。
1)平面直角坐标系统
向量在平面直角坐标系统下以两个分量进行表达,以力F为例,有:

此时若存在两个坐标系统(图1.2):坐标系一(X-Y)和坐标系二(x′-y′),不同的坐标空间,向量表达式不同。在坐标系一(X-Y)下,向量表达同上式(a);坐标系二(x′-y′)中,向量则应表达为式(b):

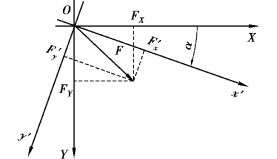
图1.2 不同平面直角坐标系下的向量表达
规定两坐标系统之间的关系为:X轴到x′轴的夹角为α,以顺时针旋转为正,可得
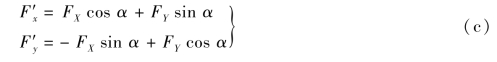
将式(c)写为矩阵形式,有
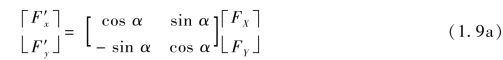
即在不同平面直角坐标系之间,向量可使用坐标变换矩阵T0进行坐标变换:
![]()
很显然,T0是一个正交矩阵,此时存在的线性变换按矩阵形式表达为:
![]()
或
![]()
2)空间直角坐标系统
式(1.9)对向量的坐标变换,可以扩展到三维空间坐标系统下。此时坐标的旋转变换独立发生在3个轴上,而非平面体系中仅对一个轴上发生。如图1.3所示,若三维空间下存在两个独立的直角坐标系统:X-Y-Z和x-y-z。x轴对应于杆始末结点i-j方向,y、z轴为杆截面上指定工程轴方向,阴影面为xy轴所在平面。(www.daowen.com)
本书所使用的直角坐标系统均约定为右手坐标系统,在一些文献中也可能使用左手坐标系统,应注意二者在空间构造时存在的区别。
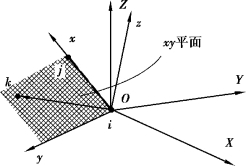
图1.3 空间直角坐标系统的旋转变换
空间直角坐标系统下,对应于坐标系X-Y-Z和x-y-z,向量的变换关系仍可写为:
![]()
正交变换矩阵T0可根据x-y-z中3个轴分别在坐标系X-Y-Z的方向余弦确定。若x轴对应于坐标系X-Y-Z的方向余弦为[l11 l12 l13],y轴的方向余弦为[l21 l22 l23],z轴的方向余弦为[l31 l32 l33],则

各轴方向余弦计算模式如下:
①点i点j为杆件的两端结点,x轴的方向余弦为[l11 l12 l13],其值根据方向ij→容易确定。若点i坐标为(Xi,Yi,Zi),点j坐标为(Xj,Yj,Zj),可直接计算ij→方向并单位化(L为ij→长度),有:
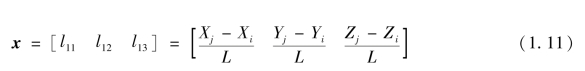
②在xy平面(图1.3中阴影区域示意)上构造任意一个不重合于x轴的向量yk,由不在x轴上的辅助点(Xk,Yk,Zk)和点i坐标(Xi,Yi,Zi)确定:
![]()
根据向量积的定义,可知[l11 l12 l13]⊗yk对应于z轴的方向。向量积写为:

对z向量单位化,则z轴相对于XYZ轴的方向余弦为:
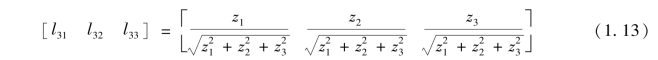
③显然,根据右手坐标系统的原则,z轴上向量叉乘x轴上向量,结果应为y轴方向上向量,故有:
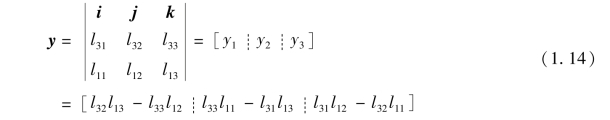
对向量单位化,则y轴相对于XYZ轴的方向余弦为:
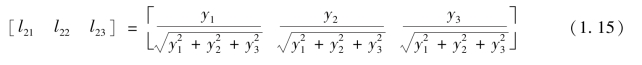
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







